
【題目】已知![]() 為實(shí)常數(shù),函數(shù)
為實(shí)常數(shù),函數(shù)![]() .
.
(1)若![]() 在
在![]() 是減函數(shù),求實(shí)數(shù)
是減函數(shù),求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)當(dāng)![]() 時(shí)函數(shù)
時(shí)函數(shù)![]() 有兩個(gè)不同的零點(diǎn)
有兩個(gè)不同的零點(diǎn)![]() ,求證:
,求證:![]() 且
且![]() .(注:
.(注:![]() 為自然對(duì)數(shù)的底數(shù));
為自然對(duì)數(shù)的底數(shù));
(3)證明![]()
【答案】(1)![]() (2)見(jiàn)解析
(2)見(jiàn)解析
【解析】分析:(1) 因![]() ,則
,則![]() ,又
,又![]() 在
在![]() 是減函數(shù)所以
是減函數(shù)所以![]() 在
在![]() 時(shí)恒成立,則實(shí)數(shù)
時(shí)恒成立,則實(shí)數(shù)![]() 的取值范圍為
的取值范圍為![]() ;(2)先證明下當(dāng)
;(2)先證明下當(dāng)![]() 時(shí),
時(shí),![]() ,由(1)知
,由(1)知![]() ,則
,則![]() 在
在![]() 內(nèi)單調(diào)遞增,在
內(nèi)單調(diào)遞增,在![]() 內(nèi)單調(diào)遞減,由
內(nèi)單調(diào)遞減,由![]() ,得
,得![]() .所以
.所以![]() ,
,![]() ;(3)由(1)知當(dāng)
;(3)由(1)知當(dāng)![]() 時(shí),
時(shí),![]() ,當(dāng)
,當(dāng)![]() 時(shí),有
時(shí),有![]() ,即
,即![]() ,累加可得結(jié)果.
,累加可得結(jié)果.
詳解:(1)因![]() ,則
,則![]() ,又
,又![]() 在
在![]() 是減函數(shù)所以
是減函數(shù)所以![]() 在
在![]() 時(shí)恒成立,則實(shí)數(shù)
時(shí)恒成立,則實(shí)數(shù)![]() 的取值范圍為
的取值范圍為![]()
(2)因當(dāng)![]() 時(shí)函數(shù)
時(shí)函數(shù)![]() 有兩個(gè)不同的零點(diǎn)
有兩個(gè)不同的零點(diǎn)![]() ,則有
,則有![]() ,
,
則有![]() .設(shè)
.設(shè)![]() .
. ![]() .
.
當(dāng)![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() ;
;
所以![]() 在
在![]() 上是增函數(shù),在
上是增函數(shù),在![]() 上是減函數(shù).
上是減函數(shù).![]() 最大值為
最大值為![]() .
.
由于![]() ,且
,且![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() .
.
下面證明:當(dāng)![]() 時(shí),
時(shí),![]() .設(shè)
.設(shè)![]() ,
,
則![]() .
.![]() 在
在![]() 上是增函數(shù),
上是增函數(shù),
所以當(dāng)![]() 時(shí),
時(shí),![]() .即當(dāng)
.即當(dāng)![]() 時(shí),
時(shí),![]() ..
..
由![]() 得
得![]() .所以
.所以![]() .
.
所以![]() ,即
,即![]() ,
,![]() ,
,![]() .
.
又![]() ,所以
,所以![]() ,
,![]() .
.
所以![]() .而
.而![]() ,則有
,則有![]() .
.
由(1)知![]() ,則
,則![]() 在
在![]() 內(nèi)單調(diào)遞增,在
內(nèi)單調(diào)遞增,在![]() 內(nèi)單調(diào)遞減,
內(nèi)單調(diào)遞減,
由![]() ,得
,得![]() .所以
.所以![]() ,
,![]() .
.
(3)由(1)知當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上是減函數(shù),且
上是減函數(shù),且![]()
所以當(dāng)![]() 時(shí)恒有
時(shí)恒有![]() ,即
,即![]()
當(dāng)![]() 時(shí),有
時(shí),有![]() ,即
,即![]() ,
,
累加得:![]() (
(![]() )
)



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
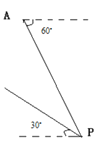
【題目】據(jù)監(jiān)測(cè),在海濱某城市附近的海面有一臺(tái)風(fēng). 臺(tái)風(fēng)中心位于城市![]() 的東偏南
的東偏南![]() 方向、距離城市
方向、距離城市![]() 的海面
的海面![]() 處,并以
處,并以![]() 的速度向西偏北
的速度向西偏北![]() 方向移動(dòng)(如圖示).如果臺(tái)風(fēng)侵襲范圍為圓形區(qū)域,半徑
方向移動(dòng)(如圖示).如果臺(tái)風(fēng)侵襲范圍為圓形區(qū)域,半徑![]() ,臺(tái)風(fēng)移動(dòng)的方向與速度不變,那么該城市受臺(tái)風(fēng)侵襲的時(shí)長(zhǎng)為_____ .
,臺(tái)風(fēng)移動(dòng)的方向與速度不變,那么該城市受臺(tái)風(fēng)侵襲的時(shí)長(zhǎng)為_____ .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面四邊形ABCD中,AD=1,CD=2,AC= ![]() .
. 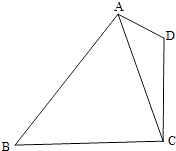
(1)求cos∠CAD的值;
(2)若cos∠BAD=﹣ ![]() ,sin∠CBA=
,sin∠CBA= ![]() ,求BC的長(zhǎng).
,求BC的長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某高級(jí)中學(xué)共有學(xué)生2000名,各年級(jí)男、女生人數(shù)如下表:
高一年級(jí) | 高二年級(jí) | 高三年級(jí) | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
已知在全校學(xué)生中隨機(jī)抽取1名,抽到高二年級(jí)女生的概率是0.19.
(1)求![]() 的值;
的值;
(2)現(xiàn)用分層抽樣的方法在全校抽取48名學(xué)生,問(wèn)應(yīng)該在高三年級(jí)抽取多少名?
(3)已知![]() ,
,![]() ,求高三年級(jí)中女生比男生多的概率.
,求高三年級(jí)中女生比男生多的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù)![]() 的一段圖象過(guò)點(diǎn)
的一段圖象過(guò)點(diǎn)![]() ,如圖所示.
,如圖所示.
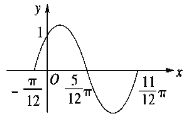
(1)求函數(shù)![]() 的表達(dá)式;
的表達(dá)式;
(2)將函數(shù)![]() 的圖象向右平移
的圖象向右平移![]() 個(gè)單位,得函數(shù)
個(gè)單位,得函數(shù)![]() 的圖象,求
的圖象,求![]() 的最大值,并求出此時(shí)自變量
的最大值,并求出此時(shí)自變量![]() 的集合,并寫(xiě)出該函數(shù)的增區(qū)間.
的集合,并寫(xiě)出該函數(shù)的增區(qū)間.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】從甲地到乙地要經(jīng)過(guò)3個(gè)十字路口,設(shè)各路口信號(hào)燈工作相互獨(dú)立,且在各路口遇到紅燈的概率分別為![]() .
.
(Ⅰ)設(shè)![]() 表示一輛車從甲地到乙地遇到紅燈的個(gè)數(shù),求隨機(jī)變量
表示一輛車從甲地到乙地遇到紅燈的個(gè)數(shù),求隨機(jī)變量![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(Ⅱ)若有2輛車獨(dú)立地從甲地到乙地,求這2輛車共遇到1個(gè)紅燈的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列命題中,正確的命題的序號(hào)為__________.
①已知隨機(jī)變量服從二項(xiàng)分布![]() ,若
,若![]() ,
,![]() ,則
,則![]() ;
;
②將一組數(shù)據(jù)中的每個(gè)數(shù)據(jù)都加上同一個(gè)常數(shù)后,方差恒不變;
③設(shè)隨機(jī)變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,若
,若![]() ,則
,則![]() ;
;
④某人在![]() 次射擊中,擊中目標(biāo)的次數(shù)為
次射擊中,擊中目標(biāo)的次數(shù)為![]() ,
,![]() ,則當(dāng)
,則當(dāng)![]() 時(shí)概率最大.
時(shí)概率最大.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2002年北京國(guó)際數(shù)學(xué)家大會(huì)會(huì)標(biāo),是以中國(guó)古代數(shù)學(xué)家趙爽的弦圖為基礎(chǔ)而設(shè)計(jì)的,弦圖用四個(gè)全等的直角三角形與一個(gè)小正方形拼成的一個(gè)大正方形![]() 如圖
如圖![]() ,若大、小正方形的面積分別為25和1,直角三角形中較大銳角為
,若大、小正方形的面積分別為25和1,直角三角形中較大銳角為![]() ,則
,則![]() 等于
等于![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com