
【題目】如圖,已知![]() ,
, ![]() 是橢圓
是橢圓![]() 的左右焦點,
的左右焦點, ![]() 為橢圓
為橢圓![]() 的上頂點,點
的上頂點,點![]() 在橢圓
在橢圓![]() 上,直線
上,直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,
, ![]() 為坐標原點,且
為坐標原點,且![]() ,
, ![]() .
.
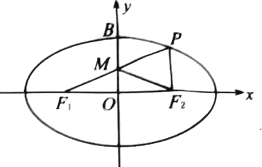
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作兩條互相垂直的直線分別與橢圓
作兩條互相垂直的直線分別與橢圓![]() 交于
交于![]() ,
, ![]() 兩點(異于點
兩點(異于點![]() ),證明:直線
),證明:直線![]() 過定點,并求該定點的坐標.
過定點,并求該定點的坐標.
【答案】(1)![]() ;(2)證明見解析,
;(2)證明見解析,  .
.
【解析】試題分析:
(1)由題意可得![]() 為
為![]() 的中位線,從而可得
的中位線,從而可得![]() ,故
,故![]() ,且
,且![]() ,然后根據(jù)
,然后根據(jù)![]() 和
和![]() 可得
可得![]() ,
, ![]() ,由此可得橢圓的方程.(2)分別設(shè)出直線直線
,由此可得橢圓的方程.(2)分別設(shè)出直線直線![]() 的方程,解方程組可得點
的方程,解方程組可得點![]() ,
, ![]() 的坐標,經(jīng)分析題意可得定點必在
的坐標,經(jīng)分析題意可得定點必在![]() 軸上,不妨設(shè)該點坐標
軸上,不妨設(shè)該點坐標![]() ,然后根據(jù)直線
,然后根據(jù)直線![]() 的斜率相等建立關(guān)于
的斜率相等建立關(guān)于![]() 的等式,結(jié)合點
的等式,結(jié)合點![]() ,
, ![]() 的坐標經(jīng)計算可得定點坐標.
的坐標經(jīng)計算可得定點坐標.
試題解析:
(1)由題意得![]() ,
,
∴![]() 為
為![]() 的中位線,
的中位線,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴橢圓方程為![]() .
.
(2)設(shè)![]() ,
, ![]() ,直線
,直線![]() :
: ![]() ,
,
由 消去y整理得
消去y整理得![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).
∴![]() ,
,
以![]() 代替上式中的
代替上式中的![]() ,可得
,可得 .
.
由題意可得,若直線![]() 關(guān)于
關(guān)于![]() 軸對稱后得到直線
軸對稱后得到直線![]() ,
,
則得到的直線![]() 與
與![]() 關(guān)于
關(guān)于![]() 軸對稱,
軸對稱,
所以若直線![]() 經(jīng)過定點,該定點一定是直線
經(jīng)過定點,該定點一定是直線![]() 與
與![]() 的交點,故該點必在
的交點,故該點必在![]() 軸上.
軸上.
設(shè)該點坐標![]() ,則有
,則有![]() ,
,
∴![]()
 ,
,
將![]() 的值代入上式,化簡得
的值代入上式,化簡得![]() ,
,
∴直線![]() 經(jīng)過定點
經(jīng)過定點 .
.


 一線名師權(quán)威作業(yè)本系列答案
一線名師權(quán)威作業(yè)本系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)擬在高一下學(xué)期開設(shè)游泳選修課,為了了解高一學(xué)生喜歡游泳是否與性別有關(guān),該學(xué)校對100名高一新生進行了問卷調(diào)查,得到如下列聯(lián)表:
喜歡游泳 | 不喜歡游泳 | 合計 | |
男生 | 10 | ||
女生 | 20 | ||
合計 |
已知在這100人中隨機抽取1人抽到喜歡游泳的學(xué)生的概率為![]() .
.
(1)請將上述列聯(lián)表補充完整;
(2)并判斷是否有99.9%的把握認為喜歡游泳與性別有關(guān)?并說明你的理由;
(3)已知在被調(diào)查的學(xué)生中有5名來自甲班,其中3名喜歡游泳,現(xiàn)從這5名學(xué)生中隨機抽取2人,求恰好有1人喜歡游泳的概率.
下面的臨界值表僅供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式: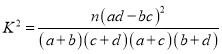 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】由于疫情影響,今年我們學(xué)校開展線上教學(xué),高一年級某班班主任為了了解學(xué)生上網(wǎng)學(xué)習(xí)時間,對本班40名學(xué)生某天上網(wǎng)學(xué)習(xí)時間進行了調(diào)查,將數(shù)據(jù)(取整數(shù))整理后,繪制出如圖所示頻率分布直方圖,已知從左到右各個小組的頻率分別是0.15,0.25,0.35,0.20,0.05,則根據(jù)直方圖所提供的信息.

(1)這一天上網(wǎng)學(xué)習(xí)時間在![]() 分鐘之間的學(xué)生有多少人?
分鐘之間的學(xué)生有多少人?
(2)這40位同學(xué)的線上平均學(xué)習(xí)時間是多少?
(3)如果只用這40名學(xué)生這一天上網(wǎng)學(xué)習(xí)時間作為樣本去推斷該校高一年級全體學(xué)生該天的上網(wǎng)學(xué)習(xí)時間,這樣推斷是否合理?為什么?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知扇形的圓心角是α,半徑為R,弧長為l.
(1)若α=75°,R=12 cm,求扇形的弧長l和面積;
(2)若扇形的周長為20 cm,當(dāng)扇形的圓心角α為多少弧度時,這個扇形的面積最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列抽取樣本的方式屬于簡單隨機抽樣的個數(shù)為( )
①從無限多個個體中抽取100個個體作為樣本.
②盒子里共有80個零件,從中選出5個零件進行質(zhì)量檢驗.在抽樣操作時,從中任意拿出一個零件進行質(zhì)量檢驗后再把它放回盒子里.
③從20件玩具中一次性抽取3件進行質(zhì)量檢驗.
④某班有56名同學(xué),指定個子最高的5名同學(xué)參加學(xué)校組織的籃球賽.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(2018·長沙二模)在平面幾何中有如下結(jié)論:正三角形ABC的內(nèi)切圓面積為S1,外接圓面積為S2,則![]() .推廣到空間可以得到類似結(jié)論:已知正四面體P-ABC的內(nèi)切球體積為V1,外接球體積為V2,則
.推廣到空間可以得到類似結(jié)論:已知正四面體P-ABC的內(nèi)切球體積為V1,外接球體積為V2,則![]() =________.
=________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)2017年招聘員工,其中A、B、C、D、E五種崗位的應(yīng)聘人數(shù)、錄用人數(shù)和錄用比例(精確到1%)如下:

(Ⅰ)從表中所有應(yīng)聘人員中隨機選擇1人,試估計此人被錄用的概率;
(Ⅱ)從應(yīng)聘E崗位的6人中隨機選擇1名男性和1名女性,求這2人均被錄用的概率;
(Ⅲ)表中A、B、C、D、E各崗位的男性、女性錄用比例都接近(二者之差的絕對值不大于5%),但男性的總錄用比例卻明顯高于女性的總錄用比例.研究發(fā)現(xiàn),若只考慮其中某四種崗位,則男性、女性的總錄用比例也接近,請寫出這四種崗位.(只需寫出結(jié)論)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】大型活動即將舉行,為了做好接待工作,組委會招募了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者,調(diào)查發(fā)現(xiàn),男、女志愿者中分別有
名女志愿者,調(diào)查發(fā)現(xiàn),男、女志愿者中分別有![]() 人和
人和![]() 人喜愛運動,其余人不喜愛運動.
人喜愛運動,其余人不喜愛運動.
(1)根據(jù)以上數(shù)據(jù)完成以下![]() 列聯(lián)表:
列聯(lián)表:
喜愛運動 | 不喜愛運動 | 總計 | |
男志愿者 | |||
女志愿者 | |||
總計 |
(2)根據(jù)列聯(lián)表判斷能否有![]() ℅的把握認為性別與喜愛運動有關(guān)?
℅的把握認為性別與喜愛運動有關(guān)?
下面的臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com