
【題目】已知向量 ![]() =(an , 2n),
=(an , 2n), ![]() =(2n+1 , ﹣an+1),n∈N* , 向量
=(2n+1 , ﹣an+1),n∈N* , 向量 ![]() 與
與 ![]() 垂直,且a1=1
垂直,且a1=1
(1)求數列{an}的通項公式;
(2)若數列{bn}滿足bn=log2an+1,求數列{anbn}的前n項和Sn .
【答案】
(1)解:∵向量 ![]() 與
與 ![]() 垂直,∴2nan+1﹣2n+1an=0,
垂直,∴2nan+1﹣2n+1an=0,
即2nan+1=2n+1an,
∴ ![]() =2∴{an}是以1為首項,2為公比的等比數列
=2∴{an}是以1為首項,2為公比的等比數列
∴an=2n﹣1
(2)解:∵bn=log2a2+1,∴bn=n
∴anbn=n2n﹣1,…(8分)
∴Sn=1+2×2+3×22+…+(n﹣1)×2n﹣2+n×2n﹣1 …①
∴2Sn=1×2+2×22+…(n﹣1)×2n﹣1+n×2n …②
由①﹣②得,﹣Sn=1+2+22+…+2n﹣1﹣n×2n= ![]()
=(1﹣n)2n﹣1
∴Sn=1﹣(n+1)2n+n2n+1=1+(n﹣1)2n.
【解析】(1)由向量 ![]() 與
與 ![]() 垂直,得2nan+1=2n+1an , ∴{an}是以1為首項,2為公比的等比數列,利用等比數列的通項公式可求an(2)由anbn=n2n﹣1 , 則Sn=1+2×2+3×22+…+(n﹣1)×2n﹣2+n×2n﹣1 , 利用錯位相減法可求其和.
垂直,得2nan+1=2n+1an , ∴{an}是以1為首項,2為公比的等比數列,利用等比數列的通項公式可求an(2)由anbn=n2n﹣1 , 則Sn=1+2×2+3×22+…+(n﹣1)×2n﹣2+n×2n﹣1 , 利用錯位相減法可求其和.
【考點精析】本題主要考查了等差數列的通項公式(及其變式)和等比數列的前n項和公式的相關知識點,需要掌握通項公式:![]() 或
或![]() ;前
;前![]() 項和公式:
項和公式: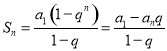 才能正確解答此題.
才能正確解答此題.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中數學 來源: 題型:
【題目】(1)求與直線3x+4y-7=0垂直,且與原點的距離為6的直線方程;
(2)求經過直線l1:2x+3y-5=0與l2:7x+15y+1=0的交點,且平行于直線x+2y-3=0的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線C: ![]() (a>0,b>0)過點A(1,0),且離心率為
(a>0,b>0)過點A(1,0),且離心率為 ![]()
(1)求雙曲線C的方程;
(2)已知直線x﹣y+m=0與雙曲線C交于不同的兩點A,B,且線段AB的中點在圓x2+y2=5上,求m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,曲線![]() ,曲線
,曲線![]() .以極點為坐標原點,極軸為
.以極點為坐標原點,極軸為![]() 軸正半軸建立平面直角坐標系
軸正半軸建立平面直角坐標系![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為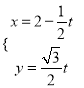 (
(![]() 為參數).
為參數).
(1)求![]() 的直角坐標方程;
的直角坐標方程;
(2)![]() 與
與![]() 交于不同的四點,這四點在
交于不同的四點,這四點在![]() 上排列順次為
上排列順次為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,把函數g(x)=f(x)﹣x的零點按從小到大的順序排列成一個數列,則該數列的通項公式為( )
,把函數g(x)=f(x)﹣x的零點按從小到大的順序排列成一個數列,則該數列的通項公式為( )
A.![]()
B.an=n﹣1
C.an=n(n﹣1)
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正項數列{an},{bn}滿足a1=3,a2=6,{bn}是等差數列,且對任意正整數n,都有 ![]() 成等比數列.
成等比數列.
(1)求數列{bn}的通項公式;
(2)設 ![]() ,試比較2Sn與
,試比較2Sn與 ![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“城市呼喚綠化”,發展園林綠化事業是促進國家經濟法陣和城市建設事業的重要組成部分,某城市響應城市綠化的號召,計劃建一如圖所示的三角形ABC形狀的主題公園,其中一邊利用現成的圍墻BC,長度為100 ![]() 米,另外兩邊AB,AC使用某種新型材料圍成,已知∠BAC=120°,AB=x,AC=y(x,y單位均為米).
米,另外兩邊AB,AC使用某種新型材料圍成,已知∠BAC=120°,AB=x,AC=y(x,y單位均為米). 
(1)求x,y滿足的關系式(指出x,y的取值范圍);
(2)在保證圍成的是三角形公園的情況下,如何設計能使所用的新型材料總長度最短?最短長度是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com