
【題目】已知函數![]() (
(![]() 為自然對數的底數).
為自然對數的底數).
(1)討論函數![]() 的單調性;
的單調性;
(2)當![]() 時,
時,![]() 恒成立,求整數
恒成立,求整數![]() 的最大值.
的最大值.
【答案】(1)見解析;(2) ![]() 的最大值為1.
的最大值為1.
【解析】
(1)根據![]() 的不同范圍,判斷導函數的符號,從而得到
的不同范圍,判斷導函數的符號,從而得到![]() 的單調性;(2)方法一:構造新函數
的單調性;(2)方法一:構造新函數![]() ,通過討論
,通過討論![]() 的范圍,判斷
的范圍,判斷![]() 單調性,從而確定結果;方法二:利用分離變量法,把問題變為
單調性,從而確定結果;方法二:利用分離變量法,把問題變為![]() ,求解函數最小值得到結果.
,求解函數最小值得到結果.
(1)![]()
![]()
當![]() 時,
時,![]()
![]() 在
在![]() 上遞增;
上遞增;
當![]() 時,令
時,令![]() ,解得:
,解得:![]()
![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增;
上遞增;
當![]() 時,
時,![]()
![]() 在
在![]() 上遞減
上遞減
(2)由題意得:![]()
即![]() 對于
對于![]() 恒成立
恒成立
方法一、令![]() ,則
,則![]()
當![]() 時,
時,![]()
![]() 在
在![]() 上遞增,且
上遞增,且![]() ,符合題意;
,符合題意;
當![]() 時,
時,![]()
![]() 時,
時,![]() 單調遞增
單調遞增
則存在![]() ,使得
,使得![]() ,且
,且![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增
上遞增 ![]()
![]()
![]()
由![]() 得:
得:![]()
又![]()
![]() 整數
整數![]() 的最大值為
的最大值為![]()
另一方面,![]() 時,
時,![]() ,
,![]()
![]() ,
,![]()
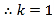 時成立
時成立
方法二、原不等式等價于:![]() 恒成立
恒成立
令![]()
![]()
令![]() ,則
,則![]()
![]() 在
在![]() 上遞增,又
上遞增,又![]() ,
,![]()
![]() 存在
存在![]() ,使得
,使得![]()
且![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增
上遞增
![]()
又![]() ,
,![]()
![]()
![]()
又![]() ,整數
,整數![]() 的最大值為
的最大值為![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】有2012位學者參加某數學會議,他們中有些人相互認識,且滿足:
(1)每個人至少認識其中的671個人;
(2)對于其中任意兩個人![]() 、
、![]() ,若
,若![]() 、
、![]() 相互不認識,則總可以通過其他人間接認識,即存在
相互不認識,則總可以通過其他人間接認識,即存在![]() ,使得
,使得![]() 認識
認識![]() ,
,![]() 認識
認識![]() ,
,![]() 認識
認識![]() ;
;
(3)不可以將2012位學者排成一排,使得相鄰的兩個人相互認識.
證明:可以將2012位學者分成兩組,其中一組能夠排成一圈,使得相鄰的人相互認識,另一組任何兩個人不認識.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,拋物線
,拋物線![]() :
: ![]() 與拋物線
與拋物線![]() :
: ![]() 異于原點
異于原點![]() 的交點為
的交點為![]() ,且拋物線
,且拋物線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
(1)若直線![]() 與拋物線
與拋物線![]() 交于點
交于點![]() ,
, ![]() ,且
,且![]() ,求
,求![]() ;
;
(2)證明: ![]() 的面積與四邊形
的面積與四邊形![]() 的面積之比為定值.
的面積之比為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩地相距![]() ,汽車從甲地勻速行駛到乙地,速度不超過
,汽車從甲地勻速行駛到乙地,速度不超過![]() .已知汽車每小時的運輸成本(以元為單位)由可變部分和固定部分組成:可變部分與速度
.已知汽車每小時的運輸成本(以元為單位)由可變部分和固定部分組成:可變部分與速度![]() (單位:
(單位:![]() )的平方成正比,且比例系數為
)的平方成正比,且比例系數為![]() ,固定部分為
,固定部分為![]() 元.
元.
(1)把全程運輸成本![]() (元)表示為速度
(元)表示為速度![]() 的函數,并求出當
的函數,并求出當![]() ,
,![]() 時,汽車應以多大速度行駛,才能使得全程運輸成本最小;
時,汽車應以多大速度行駛,才能使得全程運輸成本最小;
(2)隨著汽車的折舊,運輸成本會發生一些變化,那么當![]() ,
,![]() 元,此時汽車的速度應調整為多大,才會使得運輸成本最小.
元,此時汽車的速度應調整為多大,才會使得運輸成本最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某運動員每次射擊命中不低于8環的概率為![]() ,命中8環以下的概率為
,命中8環以下的概率為![]() ,現用隨機模擬的方法估計該運動員三次射擊中有兩次命中不低于8環,一次命中8環以下的概率:先用計算器產生0至9之間取整數值的隨機數.指定0、1、2、3、4、5表示命中不低于8環,6、7、8、9表示命中8環以下,再以三個隨機數作為一組.代表三次射擊的結果,產生如下20組隨機數:
,現用隨機模擬的方法估計該運動員三次射擊中有兩次命中不低于8環,一次命中8環以下的概率:先用計算器產生0至9之間取整數值的隨機數.指定0、1、2、3、4、5表示命中不低于8環,6、7、8、9表示命中8環以下,再以三個隨機數作為一組.代表三次射擊的結果,產生如下20組隨機數:
524207443815510013429966027954
576086324409472796544917460962
據此估計,該運動員三次射擊中有兩次命中不低于8環,一次命中8環以下的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型電器企業,為了解組裝車間職工的生活情況,從中隨機抽取了![]() 名職工進行測試,得到頻數分布表如下:
名職工進行測試,得到頻數分布表如下:
日組裝個數 |
|
|
|
|
|
|
人數 | 6 | 12 | 34 | 30 | 10 | 8 |
(1)現從參與測試的日組裝個數少于![]() 的職工中任意選取
的職工中任意選取![]() 人,求至少有
人,求至少有![]() 人日組裝個數少于
人日組裝個數少于![]() 的概率;
的概率;
(2)由頻數分布表可以認為,此次測試得到的日組裝個數![]() 服從正態分布
服從正態分布![]() ,
,![]() 近似為這
近似為這![]() 人得分的平均值(同一組數據用該組區間的中點值作為代表).
人得分的平均值(同一組數據用該組區間的中點值作為代表).
(![]() 名職工,求日組裝個數超過
名職工,求日組裝個數超過![]() 的職工人數;
的職工人數;
(ii)為鼓勵職工提高技能,企業決定對日組裝個數超過![]() 的職工日工資增加
的職工日工資增加![]() 元,若在組裝車間所有職工中任意選取
元,若在組裝車間所有職工中任意選取![]() 人,求這三人增加的日工資總額的期望.
人,求這三人增加的日工資總額的期望.
附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)當a>0時,求函數f(x)的單調區間;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com