
【題目】(1)在圓中有這樣的結(jié)論:對(duì)圓![]() 上任意一點(diǎn)
上任意一點(diǎn)![]() ,設(shè)
,設(shè)![]() 、
、![]() 是圓和
是圓和![]() 軸的兩交點(diǎn),且直線
軸的兩交點(diǎn),且直線![]() 和
和![]() 的斜率都存在,則它們的斜率之積為定值-1.試將該結(jié)論類比到橢圓
的斜率都存在,則它們的斜率之積為定值-1.試將該結(jié)論類比到橢圓![]() ,并給出證明.
,并給出證明.
(2)已知橢圓![]() ,
,![]() ,
,![]() ,設(shè)直線
,設(shè)直線![]() 與橢圓
與橢圓![]() 交于不同于
交于不同于![]() 、
、![]() 的兩點(diǎn)
的兩點(diǎn)![]() 、
、![]() ,記直線
,記直線![]() 、
、![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() 、
、![]() .
.
(ⅰ)若直線![]() 過(guò)定點(diǎn)
過(guò)定點(diǎn)![]() ,則
,則![]() 是否為定值.若是,請(qǐng)證明;若不是,請(qǐng)說(shuō)明理由.
是否為定值.若是,請(qǐng)證明;若不是,請(qǐng)說(shuō)明理由.
(ⅱ)若![]() ,求所有整數(shù)
,求所有整數(shù)![]() ,使得直線
,使得直線![]() 變化時(shí),總有
變化時(shí),總有![]() .
.
【答案】(1)對(duì)橢圓![]() 上任意一點(diǎn)
上任意一點(diǎn)![]() ,設(shè)
,設(shè)![]() 、
、![]() 是橢圓和
是橢圓和![]() 軸的兩交點(diǎn),且直線
軸的兩交點(diǎn),且直線![]() 和
和![]() 的斜率都存在,則它們的斜率之積為定值
的斜率都存在,則它們的斜率之積為定值![]() ;證明見(jiàn)解析(2)(ⅰ)是定值;證明見(jiàn)解析(ⅱ)
;證明見(jiàn)解析(2)(ⅰ)是定值;證明見(jiàn)解析(ⅱ)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)利用類比推理得:設(shè)![]() 、
、![]() 是橢圓和
是橢圓和![]() 軸的兩交點(diǎn),
軸的兩交點(diǎn),![]() 為橢圓上任一點(diǎn),且直線
為橢圓上任一點(diǎn),且直線![]() 和
和![]() 的斜率都存在,則它們的斜率之積為定值,若設(shè)
的斜率都存在,則它們的斜率之積為定值,若設(shè)![]() ,
,![]() ,
,![]() ,然后利用斜率公式可證出結(jié)論;
,然后利用斜率公式可證出結(jié)論;
(2)由于![]() ,
,![]() 恰好是橢圓與
恰好是橢圓與![]() 軸的交點(diǎn),
軸的交點(diǎn),![]() 、
、![]() 是橢圓上任意兩點(diǎn),所以在此題的求解中利用一元二次方程的根與系數(shù)的關(guān)系,再結(jié)合(1)中得到的結(jié)論可得答案.
是橢圓上任意兩點(diǎn),所以在此題的求解中利用一元二次方程的根與系數(shù)的關(guān)系,再結(jié)合(1)中得到的結(jié)論可得答案.
(1)對(duì)橢圓![]() 上任意一點(diǎn)
上任意一點(diǎn)![]() ,設(shè)
,設(shè)![]() 、
、![]() 是橢圓和
是橢圓和![]() 軸的兩交點(diǎn),且直線
軸的兩交點(diǎn),且直線![]() 和
和![]() 的斜率都存在,則它們的斜率之積為定值
的斜率都存在,則它們的斜率之積為定值![]() ,
,
證明:設(shè)![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,
則 ,
,
(2)(ⅰ)![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,
聯(lián)立直線與橢圓方程,得![]() ,則
,則 (*)
(*)

將(*)代入,得![]() 為定值.
為定值.
(ⅱ)當(dāng)時(shí),直線![]() 過(guò)定點(diǎn)
過(guò)定點(diǎn)![]() ,其中
,其中![]() ,
,
聯(lián)立直線與橢圓方程,得![]() ,由
,由![]() ,可得
,可得![]() 或
或![]() ,
,
由(1)得![]() ,從而
,從而![]() ,
,
![]() ,
,
![]() 符合題意的整數(shù)
符合題意的整數(shù)![]() 為
為![]() ,
,![]() ,
,![]() ,
,![]() .
.


 暑假作業(yè)暑假快樂(lè)練西安出版社系列答案
暑假作業(yè)暑假快樂(lè)練西安出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】經(jīng)調(diào)查統(tǒng)計(jì),網(wǎng)民在網(wǎng)上光顧某淘寶小店,經(jīng)過(guò)一番瀏覽后,對(duì)該店鋪中的![]() 三種商品有購(gòu)買意向.該淘寶小店推出買一種送5元優(yōu)惠券的活動(dòng).已知某網(wǎng)民購(gòu)買
三種商品有購(gòu)買意向.該淘寶小店推出買一種送5元優(yōu)惠券的活動(dòng).已知某網(wǎng)民購(gòu)買![]() 商品的概率分別為
商品的概率分別為![]() ,
,![]() ,
,![]() ,至少購(gòu)買一種的概率為
,至少購(gòu)買一種的概率為![]() ,最多購(gòu)買兩種的概率為
,最多購(gòu)買兩種的概率為![]() .假設(shè)該網(wǎng)民是否購(gòu)買這三種商品相互獨(dú)立.
.假設(shè)該網(wǎng)民是否購(gòu)買這三種商品相互獨(dú)立.
(1)求該網(wǎng)民分別購(gòu)買![]() 兩種商品的概率;
兩種商品的概率;
(2)用隨機(jī)變量![]() 表示該網(wǎng)民購(gòu)買商品所享受的優(yōu)惠券錢數(shù),求
表示該網(wǎng)民購(gòu)買商品所享受的優(yōu)惠券錢數(shù),求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某校高二年級(jí)某班的數(shù)學(xué)課外活動(dòng)小組有6名男生,4名女生,從中選出4人參加數(shù)學(xué)競(jìng)賽考試,用X表示其中男生的人數(shù).
(1)請(qǐng)列出X的分布列;
(2)根據(jù)你所列的分布列求選出的4人中至少有3名男生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了打好脫貧攻堅(jiān)戰(zhàn),某貧困縣農(nóng)科院針對(duì)玉米種植情況進(jìn)行調(diào)研,力爭(zhēng)有效地改良玉米品種,為農(nóng)民提供技術(shù)支援,現(xiàn)對(duì)已選出的一組玉米的莖高進(jìn)行統(tǒng)計(jì),獲得莖葉圖如圖(單位:厘米),設(shè)莖高大于或等于180厘米的玉米為高莖玉米,否則為矮莖玉米.

(1)求出易倒伏玉米莖高的中位數(shù)![]() ;
;
(2)根據(jù)莖葉圖的數(shù)據(jù),完成下面的列聯(lián)表:
抗倒伏 | 易倒伏 | |
矮莖 | ||
高莖 |
(3)根據(jù)(2)中的列聯(lián)表,是否可以在犯錯(cuò)誤的概率不超過(guò)1%的前提下,認(rèn)為抗倒伏與玉米矮莖有關(guān)?
附: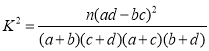 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 在
在![]() 上的最大值和最小值:
上的最大值和最小值:
(2)若![]() ,
,![]() 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某保險(xiǎn)公司為客戶定制了5個(gè)險(xiǎn)種:甲,一年期短險(xiǎn);乙,兩全保險(xiǎn);丙,理財(cái)類保險(xiǎn);丁,定期壽險(xiǎn):戊,重大疾病保險(xiǎn),各種保險(xiǎn)按相關(guān)約定進(jìn)行參保與理賠.該保險(xiǎn)公司對(duì)5個(gè)險(xiǎn)種參保客戶進(jìn)行抽樣調(diào)查,得出如下的統(tǒng)計(jì)圖例,以下四個(gè)選項(xiàng)錯(cuò)誤的是( )
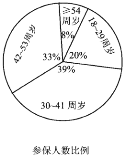
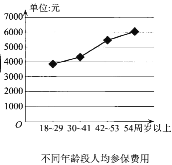
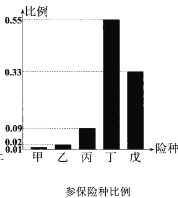
A.54周歲以上參保人數(shù)最少B.18~29周歲人群參保總費(fèi)用最少
C.丁險(xiǎn)種更受參保人青睞D.30周歲以上的人群約占參保人群的80%
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】依據(jù)某地某條河流8月份的水文觀測(cè)點(diǎn)的歷史統(tǒng)計(jì)數(shù)據(jù)所繪制的頻率分布直方圖如圖(甲)所示;依據(jù)當(dāng)?shù)氐牡刭|(zhì)構(gòu)造,得到水位與災(zāi)害等級(jí)的頻率分布條形圖如圖(乙)所示.
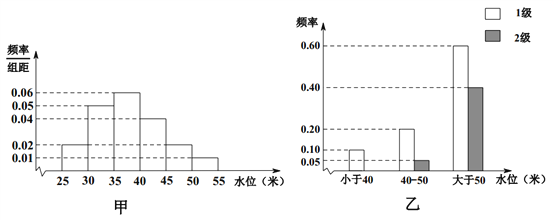
試估計(jì)該河流在8月份水位的中位數(shù);
(1)以此頻率作為概率,試估計(jì)該河流在8月份發(fā)生1級(jí)災(zāi)害的概率;
(2)該河流域某企業(yè),在8月份,若沒(méi)受1、2級(jí)災(zāi)害影響,利潤(rùn)為500萬(wàn)元;若受1級(jí)災(zāi)害影響,則虧損100萬(wàn)元;若受2級(jí)災(zāi)害影響則虧損1000萬(wàn)元.
現(xiàn)此企業(yè)有如下三種應(yīng)對(duì)方案:
方案 | 防控等級(jí) | 費(fèi)用(單位:萬(wàn)元) |
方案一 | 無(wú)措施 | 0 |
方案二 | 防控1級(jí)災(zāi)害 | 40 |
方案三 | 防控2級(jí)災(zāi)害 | 100 |
試問(wèn),如僅從利潤(rùn)考慮,該企業(yè)應(yīng)選擇這三種方案中的哪種方案?說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在①![]() .②
.②![]() 的面積
的面積![]() ,③
,③![]() 這三個(gè)條件中任選一個(gè),補(bǔ)充在下面問(wèn)題中,問(wèn)題中的
這三個(gè)條件中任選一個(gè),補(bǔ)充在下面問(wèn)題中,問(wèn)題中的![]() 是否為等邊三角形,請(qǐng)說(shuō)明理由.在
是否為等邊三角形,請(qǐng)說(shuō)明理由.在![]() 中,
中,![]() 分別為內(nèi)角
分別為內(nèi)角![]() 的對(duì)邊,且
的對(duì)邊,且![]() ,________,試判斷
,________,試判斷![]() 是否為等邊三角形?(注:如果選擇多個(gè)條件分別解答,按第一個(gè)解答計(jì)分)
是否為等邊三角形?(注:如果選擇多個(gè)條件分別解答,按第一個(gè)解答計(jì)分)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】有關(guān)獨(dú)立性檢驗(yàn)的四個(gè)命題,其中正確的是( )
A.兩個(gè)變量的2×2列聯(lián)表中,對(duì)角線上數(shù)據(jù)的乘積相差越大,說(shuō)明兩個(gè)變量有關(guān)系成立的可能性就越大
B.對(duì)分類變量X與Y的隨機(jī)變量![]() 的觀測(cè)值k來(lái)說(shuō),k越小,“X與Y有關(guān)系”的可信程度越小
的觀測(cè)值k來(lái)說(shuō),k越小,“X與Y有關(guān)系”的可信程度越小
C.從獨(dú)立性檢驗(yàn)可知:有95%的把握認(rèn)為禿頂與患心臟病有關(guān),我們說(shuō)某人禿頂,那么他有95%的可能患有心臟病
D.從獨(dú)立性檢驗(yàn)可知:有99%的把握認(rèn)為吸煙與患肺癌有關(guān),是指在犯錯(cuò)誤的概率不超過(guò)1%的前提下認(rèn)為吸煙與患肺癌有關(guān)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com