
【題目】已知![]() .
.
(1)當(dāng)![]() 時,求
時,求![]() 的極值;
的極值;
(2)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)若![]() 有2個不同零點,求實數(shù)a的取值范圍.
有2個不同零點,求實數(shù)a的取值范圍.
【答案】(1)最大值![]() ,最小值
,最小值![]() ;(2)見解析;(3)
;(2)見解析;(3)![]()
【解析】
(1)求出導(dǎo)函數(shù)![]() ,求出
,求出![]() 的解,列表確定
的解,列表確定![]() 在正負(fù),從而確定
在正負(fù),從而確定![]() 的單調(diào)性,得極值;
的單調(diào)性,得極值;
(2)根據(jù)導(dǎo)函數(shù)![]() ,對
,對![]() 分類討論:
分類討論:![]() ,
,![]() ,
,![]() 時,求出
時,求出![]() 解,再由解的大小分類討論得單調(diào)區(qū)間;
解,再由解的大小分類討論得單調(diào)區(qū)間;
(3)根據(jù)(2)所得單調(diào)性,結(jié)合零點存在定理可得結(jié)論.
![]() ,
,
(1)當(dāng)![]() 時,
時,![]() ,令
,令![]() 得
得![]() 或1
或1
|
| 0 |
| 1 |
|
| + | 0 | - | 0 | + |
|
| 極大值 |
| 極小值 |
|
∴![]() ,
,![]()
(2)![]() ,
,
①當(dāng)![]() 時,因為
時,因為![]() ,所以
,所以![]() ,
,
令![]() 得:
得:![]() ,令
,令![]() 得:
得:![]()
所以,所以![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減
上單調(diào)遞減
②當(dāng)![]() 時,令
時,令![]() 得,
得,![]() 或
或![]()
1°![]() 即
即![]() 時,
時,![]() 或
或![]() 解時,
解時,![]() ,
,![]() 時,
時,![]()
所以![]() 在
在![]() ,
,![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞增
上單調(diào)遞增
2°![]() 即
即![]() 時,
時,![]() 在R上恒成立,所以
在R上恒成立,所以![]() 在
在![]() 上單調(diào)遞增
上單調(diào)遞增
3°![]() 即
即![]() 時,
時,![]() 或
或![]() 時,
時,
![]() ,
,![]() 時,
時,![]()
所以![]() 在
在![]() ,
,![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞增
上單調(diào)遞增
綜上所述,
當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減
上單調(diào)遞減
當(dāng)![]() 時,
時,![]() 在
在![]() ,
,![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞增
上單調(diào)遞增
當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增
上單調(diào)遞增
當(dāng)![]() 時,
時,![]() 在
在![]() ,
,![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞增
上單調(diào)遞增
(3)![]()
1°當(dāng)![]() 時,
時,![]() ,只有一個零點
,只有一個零點![]() ;
;
2°當(dāng)![]() 時,由(2)可知
時,由(2)可知
![]() ,
,![]() ,
,![]() 為減函數(shù),
為減函數(shù),![]() ,
,![]() ,
,![]() 為增函數(shù)
為增函數(shù)
所以![]() 而
而![]() ,
,
所以,當(dāng)![]() 時,
時,![]() ,使
,使![]() ,
,
當(dāng)![]() 時,
時,![]() ,所以
,所以![]() ,
,
所以![]()
取![]() ,則
,則![]() ,
,
所以![]() ,所以函數(shù)有2個零點.
,所以函數(shù)有2個零點.
3°當(dāng)![]() 時,
時,![]() ,令
,令![]() 得
得![]() ,
,![]()
①![]() ,即
,即![]() 時,由(2)可得:
時,由(2)可得:![]() ,
,
∴函數(shù)![]() 至多有一個零點,不符合題意;
至多有一個零點,不符合題意;
②![]() 時,
時,![]() ,
,![]() 在
在![]() 單調(diào)遞增,
單調(diào)遞增,
所以![]() 至多有一個零點,不合題意
至多有一個零點,不合題意
③當(dāng)![]() 時,即
時,即![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,![]() .
.
所以,函數(shù)![]() 至多有1個零點
至多有1個零點
綜上:a的取值范圍是![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】以下莖葉圖記錄了甲、乙兩組各四名同學(xué)的植樹棵數(shù)。乙組記錄中有一個數(shù)據(jù)模糊,無法確認(rèn),在圖中經(jīng)X表示。
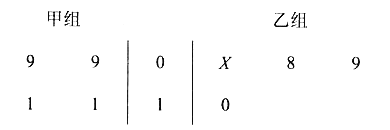
(1)如果X=8,求乙組同學(xué)植樹棵數(shù)的平均數(shù)和方差
(2)如果X=9,分別從甲、乙兩組中隨機選取一名同學(xué),求這兩名同學(xué)的植樹總棵數(shù)為19的概率
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 圖象相鄰兩條對稱軸的距離為
圖象相鄰兩條對稱軸的距離為![]() ,將函數(shù)
,將函數(shù)![]() 的圖象向左平移
的圖象向左平移![]() 個單位后,得到的圖象關(guān)于y軸對稱則函數(shù)
個單位后,得到的圖象關(guān)于y軸對稱則函數(shù)![]() 的圖象( )
的圖象( )
A. 關(guān)于直線![]() 對稱 B. 關(guān)于直線
對稱 B. 關(guān)于直線![]() 對稱
對稱
C. 關(guān)于點![]() 對稱 D. 關(guān)于點
對稱 D. 關(guān)于點![]() 對稱
對稱
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() =
=![]() ,
,![]() ;
;
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)若不等式![]() ≥
≥![]() 在(0,1)上恒成立,求實數(shù)a的取值范圍.
在(0,1)上恒成立,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題正確的是( )
A. 命題“若![]() ,則
,則![]() ”的逆否命題為真命題;
”的逆否命題為真命題;
B. 命題“![]() ”為假命題,則命題
”為假命題,則命題![]() 與命題
與命題![]() 都是假命題;
都是假命題;
C. “![]() ”是“
”是“![]() ”成立的必要不充分條件;
”成立的必要不充分條件;
D. 命題“存在![]() ,使得
,使得![]() ”的否定是:“對任意
”的否定是:“對任意![]() ,均有
,均有![]() ”.
”.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知動圓![]() 過定點
過定點![]() ,并且內(nèi)切于定圓
,并且內(nèi)切于定圓![]() ..
..
(1)求動圓圓心![]() 的軌跡方程;
的軌跡方程;
(2)若![]() 上存在兩個點
上存在兩個點![]() ,(1)中曲線上有兩個點
,(1)中曲線上有兩個點![]() ,并且
,并且![]() 三點共線,
三點共線,![]() 三點共線,
三點共線,![]() ,求四邊形
,求四邊形![]() 的面積的最小值.
的面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某服裝廠生產(chǎn)一種服裝,每件服裝成本為40元,出廠單價定為60元,該廠為鼓勵銷售商訂購,規(guī)定當(dāng)一次訂購量超過100件時,每多訂購一件,訂購的全部服裝的出廠單價就降低![]() 元,根據(jù)市場調(diào)查,銷售商一次訂購不會超過600件.
元,根據(jù)市場調(diào)查,銷售商一次訂購不會超過600件.
(1)設(shè)一次訂購![]() 件,服裝的實際出廠單價為
件,服裝的實際出廠單價為![]() 元,寫出函數(shù)
元,寫出函數(shù)![]() 的表達(dá)式;
的表達(dá)式;
(2)當(dāng)銷售商一次訂購多少件服裝時,該廠獲得的利潤最大?其最大利潤是多少?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com