
【題目】設曲線![]()
![]() ,點
,點![]() 為
為![]() 的焦點,過點
的焦點,過點![]() 作斜率為1的直線
作斜率為1的直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,點
兩點,點![]() ,
,![]() 的橫坐標的倒數和為-1.
的橫坐標的倒數和為-1.
(1)求曲線![]() 的標準方程;
的標準方程;
(2)過焦點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,分別以點
兩點,分別以點![]() ,
,![]() 為切點作曲線
為切點作曲線![]() 的切線相交于點
的切線相交于點![]() ,過點
,過點![]() 作
作![]() 軸的垂線交
軸的垂線交![]() 軸于點
軸于點![]() ,求三角形
,求三角形![]() 面積的最小值.
面積的最小值.
科目:高中數學 來源: 題型:
【題目】為了緩解城市交通壓力,某市市政府在市區一主要交通干道修建高架橋,兩端的橋墩現已建好,已知這兩橋墩相距m米,“余下的工程”只需建兩端橋墩之間的橋面和橋墩.經測算,一個橋墩的工程費用為256萬元;距離為x米的相鄰兩墩之間的橋面工程費用為(2+![]() )x萬元.假設橋墩等距離分布,所有橋墩都視為點,且不考慮其他因素.記“余下工程”的費用為y萬元.
)x萬元.假設橋墩等距離分布,所有橋墩都視為點,且不考慮其他因素.記“余下工程”的費用為y萬元.
(1)試寫出工程費用y關于x的函數關系式;
(2)當m=640米時,需新建多少個橋墩才能使工程費用y最小?并求出其最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C的參數方程為![]() (α為參數),以坐標原點為極點,x軸正半軸為極軸建立極坐標系.直線1的極坐標方程為
(α為參數),以坐標原點為極點,x軸正半軸為極軸建立極坐標系.直線1的極坐標方程為![]() .
.
(Ⅰ)求C的普通方程和l的直角坐標方程;
(Ⅱ)設直線l與x軸和y軸的交點分別為A,B,點M在曲線C上,求△MAB面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:①若線性回歸方程為![]() ,則當變量
,則當變量![]() 增加一個單位時,
增加一個單位時,![]() 一定增加3個單位;②將一組數據中的每個數據都加上同一個常數后,方差不會改變;③線性回歸直線方程
一定增加3個單位;②將一組數據中的每個數據都加上同一個常數后,方差不會改變;③線性回歸直線方程![]() 必過點
必過點![]() ;④抽簽法屬于簡單隨機抽樣;其中錯誤的說法是( )
;④抽簽法屬于簡單隨機抽樣;其中錯誤的說法是( )
A.①③B.②③④C.①D.①②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年11月5日至10日,首屆中國國際進口博覽會在國家會展中心(上海)舉行,吸引過來58個“一帶一路”沿線國家的超過1000多家企業參展,成為共建“一帶一路”的又一個重要支撐。某企業為了參加這次盛會,提升行業競爭力,加大了科技投入;該企業連續6年來得科技投入![]() (百萬元)與收益
(百萬元)與收益![]() (百萬元)的數據統計如下:
(百萬元)的數據統計如下:

根據散點圖的特點,甲認為樣本點分布在指數曲線![]() 的周圍,據此他對數據進行了一些初步處理,如下表:
的周圍,據此他對數據進行了一些初步處理,如下表:

其中![]() ,
,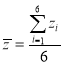 .
.
(1)(![]() )請根據表中數據,建立
)請根據表中數據,建立![]() 關于
關于![]() 的回歸方程(保留一位小數);
的回歸方程(保留一位小數);
(![]() )根據所建立回歸方程,若該企業想在下一年的收益達到2億,則科技投入的費用至少要多少(其中
)根據所建立回歸方程,若該企業想在下一年的收益達到2億,則科技投入的費用至少要多少(其中![]() )?
)?
(2)乙認為樣本點分布在二次曲線![]() 的周圍,并計算得回歸方程為
的周圍,并計算得回歸方程為![]() ,以及該回歸模型的相關指數
,以及該回歸模型的相關指數![]() ,試比較甲乙兩位員工所建立的模型,誰的擬合效果更好.
,試比較甲乙兩位員工所建立的模型,誰的擬合效果更好.
附:對于一組數據![]() ,
,![]() ,……
,……![]() ,其回歸直線方程
,其回歸直線方程![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為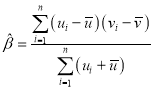 ,
,![]() ,相關指數:
,相關指數: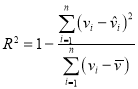 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=f(x),x∈[1,+∞),數列{an}滿足![]() ,
,
①函數f(x)是增函數;
②數列{an}是遞增數列.
寫出一個滿足①的函數f(x)的解析式______.
寫出一個滿足②但不滿足①的函數f(x)的解析式______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋子中有四個小球,分別寫有“美、麗、華、一”四個字,有放回地從中任取一個小球,直到“華”“一”兩個字都取到就停止,用隨機模擬的方法估計恰好在第四次停止的概率.利用計算機隨機產生0到3之間取整數值的隨機數,分別用0,1,2,3代表“美、麗、華、一”這四個字,以每四個隨機數為一組,表示取球四次的結果,經隨機模擬產生了以下20組隨機數:
2323 3211 2303 1233 0211 1322 2201 2213 0012 1231
2312 1300 2331 0312 1223 1031 3020 3223 3301 3212
由此可以估計,恰好第四次就停止的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com