
【題目】已知函數![]() ,設
,設![]() 為曲線
為曲線![]() 在點
在點![]() 處的切線,其中
處的切線,其中![]() .
.
(Ⅰ)求直線![]() 的方程(用
的方程(用![]() 表示);
表示);
(Ⅱ)求直線![]() 在
在![]() 軸上的截距的取值范圍;
軸上的截距的取值范圍;
(Ⅲ)設直線![]() 分別與曲線
分別與曲線![]() 和射線
和射線![]() (
(![]() )交于
)交于![]() ,
, ![]() 兩點,求
兩點,求![]() 的最小值及此時
的最小值及此時![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ)![]() ,
, ![]() .
.
【解析】試題分析:(Ⅰ) 對![]() 求導數
求導數![]() ,由此得切線
,由此得切線![]() 的方程為:
的方程為: ![]() .
.
(Ⅱ)由(Ⅰ)得,直線![]() 在
在![]() 軸上的截距為
軸上的截距為![]() .設新的函數
.設新的函數![]() ,
, ![]() 求導,求最值即可.
求導,求最值即可.
(Ⅲ)過![]() 作
作![]() 軸的垂線,與射線
軸的垂線,與射線![]() 交于點
交于點![]() ,得到△
,得到△![]() 是等腰直角三角形,
是等腰直角三角形, ![]() .設
.設 ![]() ,
, ![]() 求最值即可.
求最值即可.
試題解析:
(Ⅰ) 對![]() 求導數,得
求導數,得![]() , 所以切線
, 所以切線![]() 的斜率為
的斜率為![]() ,由此得切線
,由此得切線![]() 的方程為:
的方程為: ![]() , 即
, 即 ![]() .
.
(Ⅱ) 由(Ⅰ)得,直線![]() 在
在![]() 軸上的截距為
軸上的截距為![]() .
.
設 ![]() ,
, ![]() .所以
.所以 ![]() ,令
,令![]() ,得
,得![]() .
.
![]() ,
, ![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
|
|
|
| ||
|
| ↘ |
| ↘ |
|
所以函數![]() 在
在![]() 上單調遞減,所以
上單調遞減,所以![]() ,
, ![]() ,
,
所以直線![]() 在
在![]() 軸上的截距的取值范圍是
軸上的截距的取值范圍是![]() .
.
(Ⅲ)過![]() 作
作![]() 軸的垂線,與射線
軸的垂線,與射線![]() 交于點
交于點![]() ,
,
所以△![]() 是等腰直角三角形.所以
是等腰直角三角形.所以 ![]() .
.
設 ![]() ,
, ![]() ,
,
所以 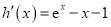 .
.
令 ![]() ,則
,則![]() ,
,
所以 ![]() 在
在![]() 上單調遞增,
上單調遞增,
所以 ![]() ,
,
從而 ![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以 ![]() ,此時
,此時![]() ,
, ![]() .
.
所以 ![]() 的最小值為
的最小值為![]() ,此時
,此時![]() .
.
點晴:本題主要考查導數與切線,導數與最值問題. 解答此類問題,應該首先確定函數的定義域,第二問中利用導數把直線![]() 在
在![]() 軸上的截距為
軸上的截距為![]() .設新的函數
.設新的函數![]() ,
, ![]() 求導,求最值即可;第三問中借助幾何關系
求導,求最值即可;第三問中借助幾何關系![]() .得到
.得到 ![]() ,
, ![]() 求最值即可.
求最值即可.


科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
: ![]() ,定點
,定點![]() (常數
(常數![]() )的直線
)的直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 、
、![]() 兩點.
兩點.
(1)若點![]() 的坐標為
的坐標為![]() ,求證:
,求證: ![]()
(2)若![]() ,以
,以![]() 為直徑的圓的位置是否恒過一定點?若存在,求出這個定點,若不存在,請說明理由.
為直徑的圓的位置是否恒過一定點?若存在,求出這個定點,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三個臭皮匠頂上一個諸葛亮,能頂得上嗎?在一次有關“三國演義”的知識競賽中,三個臭皮匠A、B、C能答對題目的概率分別為P(A)=![]() ,P(B)=
,P(B)=![]() ,P(C)=
,P(C)=![]() ,諸葛亮D能答對題目的概率為P(D)=
,諸葛亮D能答對題目的概率為P(D)=![]() ,如果將三個臭皮匠A、B、C組成一組與諸葛亮D比賽,答對題目多者為勝方,問哪方勝?
,如果將三個臭皮匠A、B、C組成一組與諸葛亮D比賽,答對題目多者為勝方,問哪方勝?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,現提供
,現提供![]() 的大致圖象的8個選項:
的大致圖象的8個選項:
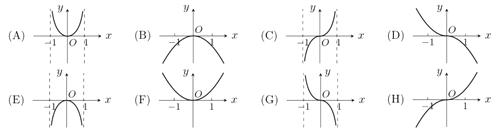
(1)請你作出選擇,你選的是( );
(2)對于函數圖像的判斷,往往只需了解函數的基本性質.為了驗證你的選擇的正確性,請你解決
下列問題:
①![]() 的定義域是___________________;
的定義域是___________________;
②就奇偶性而言, ![]() 是______________________ ;
是______________________ ;
③當![]() 時,
時, ![]() 的符號為正還是負?并證明你的結論.
的符號為正還是負?并證明你的結論.
(解決了上述三個問題,你要調整你的選項,還來得及.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為正方形,
為正方形, ![]() 底面
底面![]() ,
, ![]() ,過點
,過點![]() 的平面與棱
的平面與棱![]() ,
, ![]() ,
, ![]() 分別交于點
分別交于點![]() ,
, ![]() ,
, ![]() (
(![]() ,
, ![]() ,
, ![]() 三點均不在棱的端點處).
三點均不在棱的端點處).
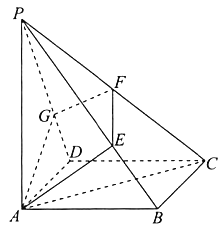
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(Ⅲ)直線![]() 是否可能與平面
是否可能與平面![]() 平行?證明你的結論.
平行?證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com