Question

【題目】函數f（x）=lnx﹣ax2+x有兩個零點，則實數a的取值范圍是（ ）
A.（0，1）
B.（﹣∞，1）
C.（﹣∞， ）
D.（0， ）

Answer 1

【答案】A
【解析】解：∵函數f（x）=lnx﹣ax2+x有兩個不同的零點， 不妨令g（x）=lnx，h（x）=ax2﹣x，
將零點問題轉化為兩個函數交點的問題；
又函數h（x）=x（ax﹣1），
當a≤0時，g（x）和h（x）只有一個交點，不滿足題意；
當a＞0時，由lnx﹣ax2+x=0，得a= ；
令r（x）= ，則r′（x）= = ，
當0＜x＜1時，r'（x）＞0，r（x）是單調增函數，
當x＞1時，r'（x）＜0，r（x）是單調減函數，且 ＞0，∴0＜a＜1；
或當a＞0時，作出兩函數g（x）=lnx，h（x）=ax2﹣x的圖象，如圖所示；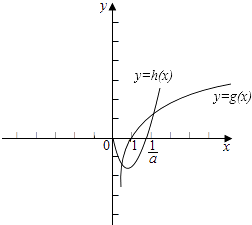
g（x）=lnx交x軸于點（1，0），
h（x）=ax2﹣x交x軸于點（0，0）和點（ ，0）；
要使方程有兩個零點，應滿足兩函數有兩個交點，
即 ＞1，解得0＜a＜1；
∴a的取值范圍是（0，1）．
故選：A．
函數f（x）=lnx﹣ax2+x有兩個不同的零點，轉化為函數g（x）=lnx和h（x）=ax2﹣x交點的問題；
討論a≤0時不滿足題意，a＞0時，求得（a）max=1，當x→+∞時，a→0，從而可得答案．
或a＞0時，作出兩函數g（x）=lnx，h（x）=ax2﹣x的圖象，由 ＞1求出a的取值范圍．