
【題目】已知函數![]() .
.
(1)若![]() 在
在![]() 上單調遞增,求實數
上單調遞增,求實數![]() 的取值范圍;
的取值范圍;
(2)設![]() ,若
,若![]() ,恒有
,恒有![]() 成立,求
成立,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由![]() 在
在![]() 上單調遞增,可得
上單調遞增,可得![]() 在
在![]() 上恒成立,利用分離參數法求出
上恒成立,利用分離參數法求出![]() 的范圍即可;
的范圍即可;
(2)設![]() ,
,![]() ,根據條件求出
,根據條件求出![]() 的范圍后,根據
的范圍后,根據![]() ,可得
,可得![]() 的最小值.
的最小值.
解:(1)由![]() ,得
,得![]() ,
,
由![]() 在
在![]() 上單調遞增,可得
上單調遞增,可得![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
當![]() 時,
時,![]() ;當
;當![]() ,則
,則![]() ,∴
,∴![]() ,
,
∴![]() 的取值范圍為
的取值范圍為![]() .
.
(2)設![]() ,
,![]() ,
,
則![]() .
.
設![]() ,則
,則![]() ,
,
∴![]() 單調遞增,即
單調遞增,即![]() 在
在![]() 上單調遞增,
上單調遞增,
∴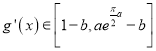 .
.
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增,∴
上單調遞增,∴![]() ,不符合題意;
,不符合題意;
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞減,
上單調遞減,![]() ,符合題意;
,符合題意;
當![]() 時,由于
時,由于![]() 為一個單調遞增的函數,
為一個單調遞增的函數,
而![]() ,
,![]() ,
,
由零點存在性定理,必存在一個零點![]() ,使得
,使得![]() ,
,
從而![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
因此只需![]() ,∴
,∴![]() ,
,
∴![]() ,從而
,從而![]() ,
,
綜上,![]() 的取值范圍為
的取值范圍為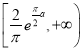 ,
,
因此![]() .
.
設![]() ,則
,則![]() ,
,
令![]() ,則
,則![]() ,
,
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
從而![]() ,
,
∴![]() 的最小值為
的最小值為![]() .
.


 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側面
中,側面![]() 為等邊三角形,且垂直于底面
為等邊三角形,且垂直于底面![]() ,
,![]() ,
,![]() 分別是
分別是![]() 的中點.
的中點.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)已知點![]() 在棱
在棱![]() 上且
上且![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在學習強國活動中,某市圖書館的科技類圖書和時政類圖書是市民借閱的熱門圖書.為了豐富圖書資源,現對已借閱了科技類圖書的市民(以下簡稱為“問卷市民”)進行隨機問卷調查,若不借閱時政類圖書記1分,若借閱時政類圖書記2分,每位市民選擇是否借閱時政類圖書的概率均為![]() ,市民之間選擇意愿相互獨立.
,市民之間選擇意愿相互獨立.
(1)從問卷市民中隨機抽取4人,記總得分為隨機變量![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)(i)若從問卷市民中隨機抽取![]() 人,記總分恰為
人,記總分恰為![]() 分的概率為
分的概率為![]() ,求數列
,求數列![]() 的前10項和;
的前10項和;
(ⅱ)在對所有問卷市民進行隨機問卷調查過程中,記已調查過的累計得分恰為![]() 分的概率為
分的概率為![]() (比如:
(比如:![]() 表示累計得分為1分的概率,
表示累計得分為1分的概率,![]() 表示累計得分為2分的概率,
表示累計得分為2分的概率,![]() ),試探求
),試探求![]() 與
與![]() 之間的關系,并求數列
之間的關系,并求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
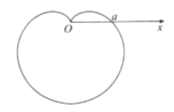
【題目】據說,年過半百的笛卡爾擔任瑞典一小公國的公主克里斯蒂娜的數學老師,日久生情,彼此愛慕,其父國王知情后大怒,將笛卡爾流放回法國,并軟禁公主,笛卡爾回法國后染上黑死病,連連給公主寫信,死前最后一封信只有一個公式:![]()
![]() 國王不懂,將這封信交給了公主,公主用笛卡爾教她的坐標知識,畫出了這個圖形“心形線”.明白了笛卡爾的心意,登上了國王寶座后,派人去尋笛卡爾,其逝久矣(僅是一個傳說).心形線是由一個圓上的一個定點,當該圓繞著與其相切且半徑相同的另外一個圓周上滾動時,這個定點的軌跡,因其形狀像心形而得名.在極坐標系
國王不懂,將這封信交給了公主,公主用笛卡爾教她的坐標知識,畫出了這個圖形“心形線”.明白了笛卡爾的心意,登上了國王寶座后,派人去尋笛卡爾,其逝久矣(僅是一個傳說).心形線是由一個圓上的一個定點,當該圓繞著與其相切且半徑相同的另外一個圓周上滾動時,這個定點的軌跡,因其形狀像心形而得名.在極坐標系![]() 中,方程
中,方程![]()
![]() 表示的曲線
表示的曲線![]() 就是一條心形線,如圖,以極軸
就是一條心形線,如圖,以極軸![]() 所在直線為
所在直線為![]() 軸,極點
軸,極點![]() 為坐標原點的直角坐標系
為坐標原點的直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為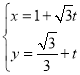 (
(![]() 為參數).
為參數).
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)若曲線![]() 與
與![]() 相交于
相交于![]() 、
、![]() 、
、![]() 三點,求線段
三點,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】每年的![]() 月
月![]() 日是全國愛牙日,為了迎接這一節日,某地區衛生部門成立了調查小組,調查“常吃零食與患齲齒的關系”,對該地區小學六年級
日是全國愛牙日,為了迎接這一節日,某地區衛生部門成立了調查小組,調查“常吃零食與患齲齒的關系”,對該地區小學六年級![]() 名學生進行檢查,按患齲齒的不患齲齒分類,得匯總數據:不常吃零食且不患齲齒的學生有
名學生進行檢查,按患齲齒的不患齲齒分類,得匯總數據:不常吃零食且不患齲齒的學生有![]() 名,常吃零食但不患齲齒的學生有
名,常吃零食但不患齲齒的學生有![]() 名,不常吃零食但患齲齒的學生有
名,不常吃零食但患齲齒的學生有![]() 名.
名.
(1)完成答卷中的![]() 列聯表,問:能否在犯錯率不超過
列聯表,問:能否在犯錯率不超過![]() 的前提下,認為該地區學生的常吃零食與患齲齒有關系?
的前提下,認為該地區學生的常吃零食與患齲齒有關系?
(2)![]() 名區衛生部門的工作人員隨機分成兩組,每組
名區衛生部門的工作人員隨機分成兩組,每組![]() 人,一組負責數據收集,另一組負責數據處理,求工作人員甲分到負責收集數據組,工作人員乙分到負責數據處理組的概率.
人,一組負責數據收集,另一組負責數據處理,求工作人員甲分到負責收集數據組,工作人員乙分到負責數據處理組的概率.
附: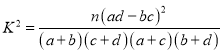
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
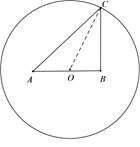
【題目】某公園準備在一圓形水池里設置兩個觀景噴泉,觀景噴泉的示意圖如圖所示,![]() 兩點為噴泉,圓心
兩點為噴泉,圓心![]() 為
為![]() 的中點,其中
的中點,其中![]() 米,半徑
米,半徑![]() 米,市民可位于水池邊緣任意一點
米,市民可位于水池邊緣任意一點![]() 處觀賞.
處觀賞.
(1)若當![]() 時,
時,![]() ,求此時
,求此時![]() 的值;
的值;
(2)設![]() ,且
,且![]() .
.
(i)試將![]() 表示為
表示為![]() 的函數,并求出
的函數,并求出![]() 的取值范圍;
的取值范圍;
(ii)若同時要求市民在水池邊緣任意一點![]() 處觀賞噴泉時,觀賞角度
處觀賞噴泉時,觀賞角度![]() 的最大值不小于
的最大值不小于![]() ,試求
,試求![]() 兩處噴泉間距離的最小值.
兩處噴泉間距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的參數方程為
的參數方程為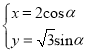 (
(![]() 為參數),在同一平面直角坐標系中,將曲線
為參數),在同一平面直角坐標系中,將曲線![]() 上的點按坐標變換
上的點按坐標變換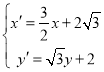 得到曲線
得到曲線![]() ,以原點為極點、
,以原點為極點、![]() 軸的正半軸為極軸,建立極坐標系.
軸的正半軸為極軸,建立極坐標系.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,與曲線
兩點,與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】曾玉、劉云、李夢、張熙四人被北京大學、清華大學、武漢大學和復旦大學錄取,他們分別被哪個學校錄取,同學們做了如下的猜想
甲同學猜:曾玉被武漢大學錄取,李夢被復旦大學錄取
同學乙猜:劉云被清華大學錄取,張熙被北京大學錄取
同學丙猜:曾玉被復旦大學錄取,李夢被清華大學錄取
同學丁猜:劉云被清華大學錄取,張熙被武漢大學錄取
結果,恰好有三位同學的猜想各對了一半,還有一位同學的猜想都不對
那么曾玉、劉云、李夢、張熙四人被錄取的大小可能是( )
A.北京大學、清華大學、復旦大學、武漢大學
B.武漢大學、清華大學、復旦大學、北京大學
C.清華大學、北京大學、武漢大學 、復旦大學
D.武漢大學、復旦大學、清華大學、北京大學
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com