Question

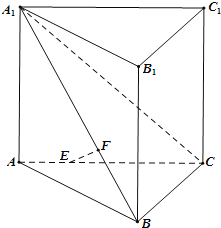
【題目】如圖，在直三棱柱側棱和底面垂直的棱柱中，平面側面，，線段AC、上分別有一點E、F且滿足，．

求證：；

求點E到直線的距離；

求二面角的平面角的余弦值．

Answer 1

【答案】（1）見解析

（2）

（3）﹣

【解析】

試題（1）過點A在平面A1ABB1內作AD⊥A1B于D，由已知條件推導出AD⊥平面A1BC，由此能證明AB⊥BC．

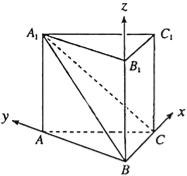
（2）以點B為坐標原點，以BC、BA、BB1所在的直線分別為x軸、y軸、z軸，建立空間直角坐標系，利用向量法能求出點E到直線A1B的距離．

（3）分別求出平面BEF的法向量和平面BEC的法向量，利用向量法能求出二面角F﹣BE﹣C的平面角的余弦值．

（1）證明：如圖，過點A在平面A1ABB1內作AD⊥A1B于D，

則由平面A1BC⊥側面A1ABB1，

且平面A1BC∩側面A1ABB1=A1B，

∴AD⊥平面A1BC，

又∵BC平面A1BC，∴AD⊥BC．

∵三棱柱ABC﹣A1B1C1是直三棱柱，∴AA1⊥底面ABC，∴AA1⊥BC．

又∵AA1∩AD=A，∴BC⊥側面A1ABB1，

又∵AB側面A1ABB1，∴AB⊥BC．（4分）

（2）解：由（1）知，以點B為坐標原點，

以BC、BA、BB1所在的直線分別為x軸、y軸、z軸，

建立如圖所示的空間直角坐標系，

B（0，0，0），A（0，3，0），C（3，0，0），A1（0，3，3）

∵線段AC、A1B上分別有一點E、F，滿足2AE=EC，2BF=FA1，

∴E（1，2，0），F（0，1，1），

∴，．

∵=0，∴EF⊥BA1，

∴點E到直線A1B的距離．（8分）

（3）解：，

設平面BEF的法向量，

則，取x=2，得=（2，﹣1，1），

由題意知平面BEC的法向量，

設二面角F﹣BE﹣C的平面角為θ，

∵θ是鈍角，∴cosθ=﹣|cos＜＞|=﹣=﹣，

∴二面角F﹣BE﹣C的平面角的余弦值為﹣．