【題目】如圖是某學校研究性課題《什么樣的活動最能促進同學們進行垃圾分類》向題的統計圖（每個受訪者都只能在問卷的5個活動中選擇一個），以下結論錯誤的是（ ）
A. 回答該問卷的總人數不可能是100個
B. 回答該問卷的受訪者中，選擇“設置分類明確的垃圾桶”的人數最多
C. 回答該問卷的受訪者中，選擇“學校團委會宣傳”的人數最少
D. 回答該問卷的受訪者中，選擇“公益廣告”的人數比選擇“學校要求”的少8個
一線名師提優試卷系列答案科目：高中數學 來源： 題型：
【題目】已知
的定義域為
，
，使得不等式
成立，關于
的不等式
的解集記為
.
（1）若
為真，求實數
的取值集合
；
（2）在（1）的條件下，若
是
的充分不必要條件，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將參加數學競賽決賽的500名同學編號為：001，002，...，500，采用系統抽樣的方法抽取一個容量為50的樣本，且隨機抽到的號碼為005，這500名學生分別在三個考點考試，從001到200在第一考點，從201到365在第二考點，從366到500在第三考點，則第二考點被抽中的人數為( )
A. 15B. 16C. 17D. 18
查看答案和解析>>
科目：高中數學 來源： 題型：
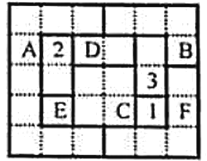
【題目】四色猜想是世界三大數學猜想之一，1976年美國數學家阿佩爾與哈肯證明了四色定理．其內容是：“任意一張平面地圖只用四種顏色就能使具有共同邊界的國家涂上不同的顏色．”用數學語言表示為“將平面任意地細分為不相重疊的區域，每一個區域總可以用1，2，3，4四個數字之一標記，而不會使相鄰的兩個區域得到相同的數字．”如圖，網格紙上小正方形的邊長為1，粗實線圍成的各區域（如區域D由兩個邊長為1的小正方形構成）上分別標有數字1，2，3，4的四色地圖符合四色定理，區域A、B、C、D、E、F標記的數字丟失若在該四色地圖上隨機取一點，則恰好取在標記為4的區域的概率是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
，
是圓
上的一個動點，
為圓心，線段
的垂直平分線與直線
的交點為
．
（1）求點的軌跡
的方程；
（2）設與
軸的正半軸交于點
，直線
與交于
兩點（
不經過點），且
,證明：直線經過定點，并寫出該定點的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，圓C經過M(1，3)，N(4，2)，P(1，﹣7)三點，且直線l：x＋ay﹣1＝0(a
R)是圓C的一條對稱軸，過點A(﹣6，a) 作圓C的一條切線，切點為B，則線段AB的長度為_______．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
