
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若![]() ,求曲線
,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)若對任意的![]() ,
,![]() ,
,![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)對![]() 求導得到
求導得到![]() ,代入
,代入![]() ,得到切線的斜率,結合切點,得到切線方程;(2)根據(jù)題意,得到
,得到切線的斜率,結合切點,得到切線方程;(2)根據(jù)題意,得到![]() ,然后利用參變分離,得到
,然后利用參變分離,得到![]() ,設
,設![]() ,利用導數(shù)得到
,利用導數(shù)得到![]() 的最小值,從而得到
的最小值,從而得到![]() 的范圍.
的范圍.
(1)因為![]() ,所以函數(shù)
,所以函數(shù)![]() ,
,
所以![]() ,即切點為
,即切點為![]()
所以![]() ,
,
代入![]() ,得到
,得到![]() ,
,
故所求的切線方程為![]() ,
,
即![]() .
.
(2)對任意的![]() ,
,![]() ,
,![]() 恒成立,
恒成立,
可得![]() ,對任意的
,對任意的![]() ,
,![]() 恒成立,
恒成立,
![]() ,令
,令![]() 得
得![]() 或
或![]() ,
,
所以![]() 時,
時,![]() ,
,![]() 單調(diào)遞減,
單調(diào)遞減,
![]() 時,
時,![]() ,
,![]() 單調(diào)遞增,
單調(diào)遞增,
而![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,對任意的
,對任意的![]() 恒成立,
恒成立,
即![]() 對任意的
對任意的![]() 恒成立,
恒成立,
所以![]() ,對任意的
,對任意的![]() 恒成立,
恒成立,
設![]() ,
,![]() ,則
,則![]()
![]() ,
,
設![]() ,
,![]()
因為![]() ,所以
,所以![]() ,所以
,所以![]() 單調(diào)遞增,
單調(diào)遞增,
即![]() 單調(diào)遞增,而
單調(diào)遞增,而![]() ,
,
所以當![]() ,
,![]() ,
,![]() 單調(diào)遞減,
單調(diào)遞減,
當![]() ,
,![]() ,
,![]() 單調(diào)遞增,
單調(diào)遞增,
所以![]() 時,
時,![]() 取得最小值,為
取得最小值,為![]() ,
,
所以![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求實數(shù)
,求實數(shù)![]() ,
,![]() 的值;
的值;
(2)若![]() ,且
,且![]() 在區(qū)間
在區(qū)間![]() 上恒成立,求實數(shù)
上恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() ,且
,且![]() ,討論函數(shù)
,討論函數(shù)![]() 的單調(diào)性.
的單調(diào)性.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,上、下頂點分別為
,上、下頂點分別為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,試探究在
兩點,試探究在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得可
,使得可![]() 為定值?若存在,求出點
為定值?若存在,求出點![]() 的坐標,若不存在,請說明理由?
的坐標,若不存在,請說明理由?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,(x>0).
,(x>0).
(1)當0<a<b,且f(a)=f(b)時,求證:ab>1;
(2)是否存在實數(shù)a,b(a<b),使得函數(shù)y=f(x)的定義域、值域都是[a,b],若存在,則求出a,b的值,若不存在,請說明理由.
(3)若存在實數(shù)a,b(a<b),使得函數(shù)y=f(x)的定義域為[a,b]時,值域為[ma,mb](m≠0),求m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某學校成立了數(shù)學、英語、音樂3個課外興趣小組,3個小組分別有39、32、33個成員,一些成員參加了不止一個小組,具體情況如圖所示.
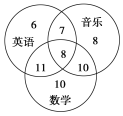
現(xiàn)隨機選取一個成員,他屬于至少2個小組的概率是________,他屬于不超過2個小組的概率是________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】數(shù)學老師給出一個函數(shù)![]() ,甲、乙、丙、丁四個同學各說出了這個函數(shù)的一條性質:甲:在
,甲、乙、丙、丁四個同學各說出了這個函數(shù)的一條性質:甲:在![]() 上函數(shù)單調(diào)遞減;乙:在
上函數(shù)單調(diào)遞減;乙:在![]() 上函數(shù)單調(diào)遞增;丙:在定義域R上函數(shù)的圖象關于直線
上函數(shù)單調(diào)遞增;丙:在定義域R上函數(shù)的圖象關于直線![]() 對稱;丁:
對稱;丁:![]() 不是函數(shù)的最小值.老師說:你們四個同學中恰好有三個人說的正確.那么,你認為____說的是錯誤的.
不是函數(shù)的最小值.老師說:你們四個同學中恰好有三個人說的正確.那么,你認為____說的是錯誤的.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】一個摸球游戲,規(guī)則如下:在一不透明的紙盒中,裝有6個大小相同、顏色各異的玻璃球.參加者交費1元可玩1次游戲,從中有放回地摸球3次.參加者預先指定盒中的某一種顏色的玻璃球,然后摸球.當所指定的玻璃球不出現(xiàn)時,游戲費被沒收;當所指定的玻璃球出現(xiàn)1次,2次,3次時,參加者可相應獲得游戲費的0倍,1倍,![]() 倍的獎勵(
倍的獎勵(![]() ),且游戲費仍退還給參加者.記參加者玩1次游戲的收益為
),且游戲費仍退還給參加者.記參加者玩1次游戲的收益為![]() 元.
元.
(1)求概率![]() 的值;
的值;
(2)為使收益![]() 的數(shù)學期望不小于0元,求
的數(shù)學期望不小于0元,求![]() 的最小值.
的最小值.
(注:概率學源于賭博,請自覺遠離不正當?shù)挠螒颍。?/span>
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在極坐標系中,圓C的圓心坐標為(1,0),半徑為1.
(1)求圓C的極坐標方程;
(2)若以極點O為原點,極軸所在直線為x軸建立平面直角坐標系.已知直線l的參數(shù)方程為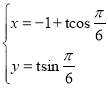 (t為參數(shù)),試判斷直線l與圓C的位置關系.
(t為參數(shù)),試判斷直線l與圓C的位置關系.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com