
【題目】將函數(shù)![]() 在區(qū)間
在區(qū)間![]() 內的全部極值點按從小到大的順序排成數(shù)列
內的全部極值點按從小到大的順序排成數(shù)列![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)設![]() ,數(shù)列
,數(shù)列![]() 的前n項和
的前n項和![]() ,求證:數(shù)列
,求證:數(shù)列![]() 為等比數(shù)列,并求
為等比數(shù)列,并求![]() .
.
【答案】(1)![]() ;(2)證明見解析,
;(2)證明見解析,![]() .
.
【解析】
(1)先利用三角函數(shù)的誘導公式及二倍角公式化簡函數(shù)![]() ,令
,令![]() 得極值點,判斷出全部極值點按從小到大排列構成以
得極值點,判斷出全部極值點按從小到大排列構成以![]() 為首項,
為首項,![]() 為公差的等差數(shù)列,用等差數(shù)列的通項公式求出通項.
為公差的等差數(shù)列,用等差數(shù)列的通項公式求出通項.
(2)利用![]() ,求出
,求出![]() ,作商
,作商![]() ,利用等比數(shù)列的定義判斷出
,利用等比數(shù)列的定義判斷出![]() 是以
是以![]() 為首項,
為首項,![]() 為公比的等比數(shù)列,利用等比數(shù)列的通項公式求出通項,一步求出數(shù)列
為公比的等比數(shù)列,利用等比數(shù)列的通項公式求出通項,一步求出數(shù)列![]() 前
前![]() 項的和.
項的和.
(1)![]()
![]()
![]()
令![]() ,即
,即![]()
所以函數(shù)![]() 的極值點為
的極值點為![]() .
.
從而函數(shù)![]() 在區(qū)間
在區(qū)間![]() 內的全部極值點按從小到大排列構成以以
內的全部極值點按從小到大排列構成以以![]() 為首項,
為首項,![]() 為公差的等差數(shù)列.
為公差的等差數(shù)列.
所以數(shù)列![]()
(2)由![]() 可知對任意的正整數(shù)
可知對任意的正整數(shù)![]() ,
,![]() 都不是
都不是![]() 的整數(shù)倍.
的整數(shù)倍.
所以![]()
![]()
所以數(shù)列![]() 為等比數(shù)列.
為等比數(shù)列.
![]()
所以![]()
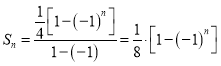 .
.


 挑戰(zhàn)100單元檢測試卷系列答案
挑戰(zhàn)100單元檢測試卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】依據(jù)某地某條河流8月份的水文觀測點的歷史統(tǒng)計數(shù)據(jù)所繪制的頻率分布直方圖如圖(甲)所示;依據(jù)當?shù)氐牡刭|構造,得到水位與災害等級的頻率分布條形圖如圖(乙)所示.
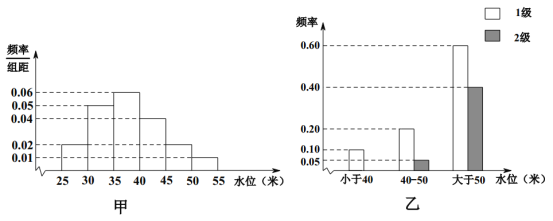
(1)試估計該河流在8月份水位的眾數(shù);
(2)我們知道若該河流8月份的水位小于40米的頻率為f,該河流8月份的水位小于40米的情況下發(fā)生1級災害的頻率為g,則該河流8月份的水位小于40且發(fā)生1級災害的頻率為![]() ,其他情況類似.據(jù)此,試分別估計該河流在8月份發(fā)生12級災害及不發(fā)生災害的頻率
,其他情況類似.據(jù)此,試分別估計該河流在8月份發(fā)生12級災害及不發(fā)生災害的頻率![]() ,
,![]() ,
,![]() ;
;
(3)該河流域某企業(yè),在8月份,若沒受12級災害影響,利潤為500萬元;若受1級災害影響,則虧損100萬元;若受2級災害影響則虧損1000萬元.現(xiàn)此企業(yè)有如下三種應對方案:
方案 | 防控等級 | 費用(單位:萬元) |
方案一 | 無措施 | 0 |
方案二 | 防控1級災害 | 40 |
方案三 | 防控2級災害 | 100 |
試問,如僅從利潤考慮,該企業(yè)應選擇這三種方案中的哪種方案?說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】經(jīng)市場調查:生產(chǎn)某產(chǎn)品需投入年固定成本為![]() 萬元,每生產(chǎn)
萬元,每生產(chǎn)![]() 萬件,需另投入流動成本為
萬件,需另投入流動成本為![]() 萬元,在年產(chǎn)量不足
萬元,在年產(chǎn)量不足![]() 萬件時,
萬件時,![]()
![]() (萬元),在年產(chǎn)量不小于
(萬元),在年產(chǎn)量不小于![]() 萬件時,
萬件時,![]() (萬元).通過市場分析,每件產(chǎn)品售價為
(萬元).通過市場分析,每件產(chǎn)品售價為![]() 元時,生產(chǎn)的商品能當年全部售完.
元時,生產(chǎn)的商品能當年全部售完.
(1)寫出年利潤![]() (萬元)關于年產(chǎn)量
(萬元)關于年產(chǎn)量![]() (萬件)的函數(shù)解析式;
(萬件)的函數(shù)解析式;
(2)當產(chǎn)量為多少時利潤最大?并求出最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,
,![]() 是實數(shù).
是實數(shù).
(Ⅰ)若![]() 在
在![]() 處取得極值,求
處取得極值,求![]() 的值;
的值;
(Ⅱ)若![]() 在區(qū)間
在區(qū)間![]() 為增函數(shù),求
為增函數(shù),求![]() 的取值范圍;
的取值范圍;
(Ⅲ)在(Ⅱ)的條件下,函數(shù)![]() 有三個零點,求
有三個零點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為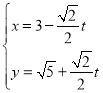 (
(![]() 為參數(shù))。在極坐標系(與直角坐標系
為參數(shù))。在極坐標系(與直角坐標系![]() 取相同的長度單位,且以原點
取相同的長度單位,且以原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸)中,圓
軸正半軸為極軸)中,圓![]() 的極坐標方程為
的極坐標方程為![]() 。
。
(1)求直線![]() 的普通方程和圓
的普通方程和圓![]() 的直角坐標方程;
的直角坐標方程;
(2)設圓![]() 與直線
與直線![]() 交于
交于![]() ,
,![]() 兩點,若點
兩點,若點![]() 的坐標為
的坐標為![]() ,求
,求![]() 。
。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知△ABC的兩個頂點A,B的坐標分別為(![]() ,0),(
,0),(![]() ,0),圓E是△ABC的內切圓,在邊AC,BC,AB上的切點分別為P,Q,R,|CP|=2
,0),圓E是△ABC的內切圓,在邊AC,BC,AB上的切點分別為P,Q,R,|CP|=2![]() ,動點C的軌跡為曲線G.
,動點C的軌跡為曲線G.
(1)求曲線G的方程;
(2)設直線l與曲線G交于M,N兩點,點D在曲線G上,![]() 是坐標原點
是坐標原點![]() ,判斷四邊形OMDN的面積是否為定值?若為定值,求出該定值;如果不是,請說明理由.
,判斷四邊形OMDN的面積是否為定值?若為定值,求出該定值;如果不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為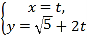 (
(![]() 為參數(shù)),以原點
為參數(shù)),以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)已知點![]() ,直線
,直線![]() 與曲線
與曲線![]() 相交于點
相交于點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】[選修4-4:極坐標與參數(shù)方程]
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 是參數(shù)),以坐標原點
是參數(shù)),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若射線![]()
![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,與曲線
兩點,與曲線![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 取最大值時
取最大值時![]() 的值
的值
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com