Question

【題目】已知函數f（x）=﹣x2+ax+4，g（x）=|x+1|+|x﹣1|．
（1）當a=1時，求不等式f（x）≥g（x）的解集；
（2）若不等式f（x）≥g（x）的解集包含[﹣1，1]，求a的取值范圍．

Answer 1

【答案】
（1）解：當a=1時，f（x）=﹣x2+x+4，是開口向下，對稱軸為x= 的二次函數，

g（x）=|x+1|+|x﹣1|= ，

當x∈（1，+∞）時，令﹣x2+x+4=2x，解得x= ，g（x）在（1，+∞）上單調遞增，f（x）在（1，+∞）上單調遞減，∴此時f（x）≥g（x）的解集為（1， ]；

當x∈[﹣1，1]時，g（x）=2，f（x）≥f（﹣1）=2．

當x∈（﹣∞，﹣1）時，g（x）單調遞減，f（x）單調遞增，且g（﹣1）=f（﹣1）=2．

綜上所述，f（x）≥g（x）的解集為[﹣1， ]

（2）解：依題意得：﹣x2+ax+4≥2在[﹣1，1]恒成立，即x2﹣ax﹣2≤0在[﹣1，1]恒成立，則只需 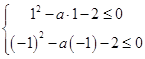，解得﹣1≤a≤1，

故a的取值范圍是[﹣1，1]

【解析】（1）當a=1時，f（x）=﹣x2+x+4，g（x）=|x+1|+|x﹣1|= 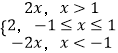，分x＞1、x∈[﹣1，1]、x∈（﹣∞，﹣1）三類討論，結合g（x）與f（x）的單調性質即可求得f（x）≥g（x）的解集為[﹣1， ]；（2）依題意得：﹣x2+ax+4≥2在[﹣1，1]恒成立x2﹣ax﹣2≤0在[﹣1，1]恒成立，只需 ，解之即可得a的取值范圍．