
【題目】對于定義域為![]() 的函數
的函數![]() ,如果存在區間
,如果存在區間![]() 滿足
滿足![]() 是
是![]() 上的單調函數,且
上的單調函數,且![]() 在區間
在區間![]() 上的值域也為
上的值域也為![]() ,則稱函數
,則稱函數![]() 為區間
為區間![]() 上的“保值函數”,
上的“保值函數”,![]() 為“保值區間”.根據此定義給出下列命題:①函數
為“保值區間”.根據此定義給出下列命題:①函數![]() 是
是![]() 上的“保值函數”;②若函數
上的“保值函數”;②若函數![]() 是
是![]() 上的“保值函數”,則
上的“保值函數”,則![]() ;③對于函數
;③對于函數![]() 存在區間
存在區間![]() ,且
,且![]() ,使函數
,使函數![]() 為
為![]() 上的“保值函數”.其中所有真命題的序號為( )
上的“保值函數”.其中所有真命題的序號為( )
A.②B.③C.①③D.②③
【答案】D
【解析】
①根據函數單調性定義和“保值函數”的概念判斷即可,②結合函數![]() 的圖象可得結論,③由導數確定函數在
的圖象可得結論,③由導數確定函數在![]() 是單調遞增的,而方程
是單調遞增的,而方程![]() 有兩個解
有兩個解![]() (
(![]() ),構造新函數
),構造新函數![]() ,由零點存在定理確定
,由零點存在定理確定![]() 的零點
的零點![]() 即可.
即可.
由“保值函數”定義可知![]() 為區間
為區間![]() 上的“保值函數”則
上的“保值函數”則![]() 在
在![]() 上是單調函數且在區間
上是單調函數且在區間![]() 時其值域也為
時其值域也為![]() ,那么當函數
,那么當函數![]() 為增函數時滿足條件
為增函數時滿足條件![]() 在
在![]() 上有兩個不同的實數解
上有兩個不同的實數解![]() ,
,![]() 的函數
的函數![]() 就是“保值函數”,
就是“保值函數”,
命題①中![]() ,雖滿足在
,雖滿足在![]() 上單調但值域為
上單調但值域為![]() ,不是
,不是![]() ,故①為假命題;
,故①為假命題;
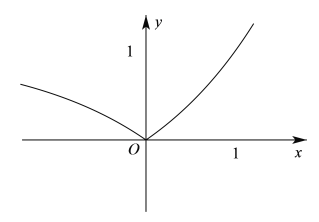
②中由![]() 的圖象可知,函數在
的圖象可知,函數在![]() 上單調且值域為
上單調且值域為![]() ,其為區間
,其為區間![]() 上的“保值函數”故②為真命題;
上的“保值函數”故②為真命題;
③中![]() ,則由
,則由![]() 在
在![]() 成立,所以
成立,所以![]() 為
為![]() 上的增函數,再由
上的增函數,再由![]() 解得有兩個根
解得有兩個根![]() ,
,![]() ,構造函數
,構造函數![]() ,
,![]() 是減函數,
是減函數,![]() ,
,![]() ,由零點存在性定理知存在
,由零點存在性定理知存在![]() ,使
,使![]() 成立,故③為真命題.綜上所有真命題的序號為②③,
成立,故③為真命題.綜上所有真命題的序號為②③,
故選:D.


 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案科目:高中數學 來源: 題型:
【題目】某網站舉行“衛生防疫”的知識競賽網上答題,共有120000人通過該網站參加了這次競賽,為了解競賽成績情況,從中抽取了100人的成績進行統計,其中成績分組區間為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其頻率分布直方圖如圖所示,請你解答下列問題:
,其頻率分布直方圖如圖所示,請你解答下列問題:
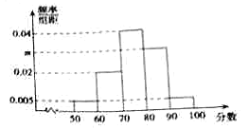
(1)求![]() 的值;
的值;
(2)成績不低于90分的人就能獲得積分獎勵,求所有參賽者中獲得獎勵的人數;
(3)根據頻率分布直方圖,估計這次知識競賽成績的平均分(用組中值代替各組數據的平均值).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右頂點為
的左右頂點為![]() ,
,![]() 為橢圓上異于
為橢圓上異于![]() 的動點,設直線
的動點,設直線![]() 的斜率分別為
的斜率分別為![]() ,且
,且![]() .
.
(1)求橢圓![]() 的離心率;
的離心率;
(2)當橢圓![]() 內切于圓
內切于圓![]() 時,設動直線
時,設動直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,
兩點,![]() 為坐標原點,若
為坐標原點,若![]() ,問:
,問:![]() 的面積是否存在最小值?若存在,求出這個最小值;若不存在,請說明理由.
的面積是否存在最小值?若存在,求出這個最小值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】科技創新能力是決定綜合國力和國際競爭力的關鍵因素,也是推動經濟實現高質量發展的重要支撐,而研發投入是科技創新的基本保障,下圖是某公司從2010年到2019年這10年研發投入的數據分布圖:

其中折線圖是該公司研發投入占當年總營收的百分比,條形圖是當年研發投入的數值(單位:十億元).
(I)從2010年至2019年中隨機選取一年,求該年研發投入占當年總營收的百分比超過10%的概率;
(II)從2010年至2019年中隨機選取兩個年份,設X表示其中研發投入超過500億元的年份的個數,求X的分布列和數學期望;
(III)根據圖中的信息,結合統計學知識,判斷該公司在發展的過程中是否比較重視研發,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐![]() 中,
中,![]() ,
,![]() 分別是線段
分別是線段![]() ,
,![]() 的中點,底面
的中點,底面![]() 是正三角形,延長
是正三角形,延長![]() 到點
到點![]() ,使得
,使得![]() .
.
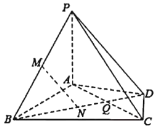
(1)![]() 為線段
為線段![]() 上確定一點,當
上確定一點,當![]() 平面
平面![]() 時,求
時,求![]() 的值;
的值;
(2)當![]() 平面
平面![]() ,且
,且![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (a∈R且a≠0).
(a∈R且a≠0).
(1)當a![]() 時,求曲線y=f(x)在點(1,f(1))處的切線方程;
時,求曲線y=f(x)在點(1,f(1))處的切線方程;
(2)討論函數f(x)的單調性與單調區間;
(3)若y=f(x)有兩個極值點x1,x2,證明:f(x1)+f(x2)<9﹣lna.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點F為橢圓![]() (a>b>0)的一個焦點,點A為橢圓的右頂點,點B為橢圓的下頂點,橢圓上任意一點到點F距離的最大值為3,最小值為1.
(a>b>0)的一個焦點,點A為橢圓的右頂點,點B為橢圓的下頂點,橢圓上任意一點到點F距離的最大值為3,最小值為1.
(1)求橢圓的標準方程;
(2)若M、N在橢圓上但不在坐標軸上,且直線AM∥直線BN,直線AN、BM的斜率分別為k1和k2,求證:k1k2=e2﹣1(e為橢圓的離心率).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國著名數學家華羅庚先生曾說:數缺形時少直觀,形缺數時難入微,數形結合百般好,隔裂分家萬事休.在數學的學習和研究中,常用函數的圖象研究函數的性質,也常用函數的解析式來琢磨函數的圖象特征.如函數![]() 的圖象大致為( )
的圖象大致為( )
A. B.
B.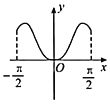
C.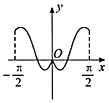 D.
D.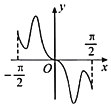
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖(1),在矩形![]() 中,
中,![]() ,
,![]() 在邊
在邊![]() 上,
上,![]() .沿
.沿![]() ,
,![]() 將
將![]() 和
和![]() 折起,使平面
折起,使平面![]() 和平面
和平面![]() 都與平面
都與平面![]() 垂直,如圖(2).
垂直,如圖(2).
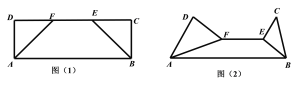
(1)試判斷圖(2)中直線![]() 與
與![]() 的位置關系,并說明理由;
的位置關系,并說明理由;
(2)求平面![]() 和平面
和平面![]() 所成銳角二面角的余弦值.
所成銳角二面角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com