
【題目】已知集合A={x|m﹣1≤x≤2m+3},函數f(x)=lg(﹣x2+2x+8)的定義域為B.
(1)當m=2時,求A∪B、(RA)∩B;
(2)若A∩B=A,求實數m的取值范圍.
【答案】
(1)解:根據題意,當m=2時,A={x|1≤x≤7},B={x|﹣2<x<4},
則A∪B={x|﹣2<x≤7},
又RA={x|x<1或x>7},
則(RA)∩B={x|﹣2<x<1}
(2)解:根據題意,若A∩B=A,則AB,
分2種情況討論:
①、當A=時,有m﹣1>2m+3,解可得m<﹣4,
②、當A≠時,
若有AB,必有 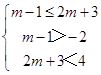 ,解可得﹣1<m<
,解可得﹣1<m< ![]() ,
,
綜上可得:m的取值范圍是:(﹣∞,﹣4)∪(﹣1, ![]() )
)
【解析】(1)根據題意,由m=2可得A={x|1≤x≤7},由并集定義可得A∪B的值,由補集定義可得RA={x|x<1或x>7},進而由交集的定義計算可得(RA)∩B,即可得答案;(2)根據題意,分析可得AB,進而分2種情況討論:①、當A=時,有m﹣1>2m+3,②、當A≠時,有 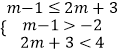 ,分別求出m的取值范圍,進而對其求并集可得答案.
,分別求出m的取值范圍,進而對其求并集可得答案.
【考點精析】解答此題的關鍵在于理解交、并、補集的混合運算的相關知識,掌握求集合的并、交、補是集合間的基本運算,運算結果仍然還是集合,區分交集與并集的關鍵是“且”與“或”,在處理有關交集與并集的問題時,常常從這兩個字眼出發去揭示、挖掘題設條件,結合Venn圖或數軸進而用集合語言表達,增強數形結合的思想方法.


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:高中數學 來源: 題型:
【題目】已知點P在直線x+3y﹣2=0上,點Q在直線x+3y+6=0上,線段PQ的中點為M(x0 , y0),且y0<x0+2,則 ![]() 的取值范圍是( )
的取值范圍是( )
A.[﹣ ![]() ,0)
,0)
B.(﹣ ![]() ,0)
,0)
C.(﹣ ![]() ,+∞)
,+∞)
D.(﹣∞,﹣ ![]() )∪(0,+∞)
)∪(0,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=a(|sinx|+|cosx|)﹣ ![]() sin2x﹣1,若f(
sin2x﹣1,若f( ![]() )=
)= ![]() ﹣
﹣ ![]() .
.
(1)求a的值,并寫出函數f(x)的最小正周期(不需證明);
(2)是否存在正整數k,使得函數f(x)在區間[0,kπ]內恰有2017個零點?若存在,求出k的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高二某班50名學生在一次百米測試中,成績全部都介于13秒到18秒之間,將測試結果按如下方式分成五組,第一組[13,14),第二組[14,15),…,第五組[17,18],如圖是按上述分組方法得到的頻率分布直方圖. 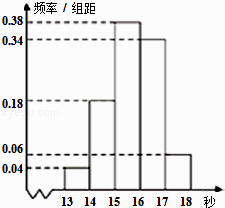
(1)若成績在區間[14,16)內規定為良好,求該班在這次百米測試中成績為良好的人數;
(2)請根據頻率分布直方圖估計樣本數據的眾數和中位數(精確到0.01).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2﹣(1+a)x+y2﹣ay+a=0(a∈R). (Ⅰ) 若a=1,求直線y=x被圓C所截得的弦長;
(Ⅱ) 若a>1,如圖,圓C與x軸相交于兩點M,N(點M在點N的左側).過點M的動直線l與圓O:x2+y2=4相交于A,B兩點.問:是否存在實數a,使得對任意的直線l均有∠ANM=∠BNM?若存在,求出實數a的值,若不存在,請說明理由.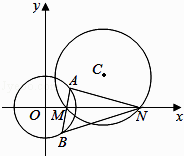
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:x∈R,cosx=2;命題q:x∈R,x2﹣x+1>0,則下列結論中正確的是( )
A.p∨q是假命題
B.p∧q是真命題
C.(¬p)∧(¬q)是真命題
D.(¬p)∨(¬q)是真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(ωx﹣ ![]() )(
)( ![]() <ω<2),在區間(0,
<ω<2),在區間(0, ![]() )上( )
)上( )
A.既有最大值又有最小值
B.有最大值沒有最小值
C.有最小值沒有最大值
D.既沒有最大值也沒有最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合M={x|﹣a<x<a+1,a∈R},集合N={x|x2﹣2x﹣3≤0}.
(1)當a=1時,求M∪N及N∩RM;
(2)若x∈M是x∈N的充分條件,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com