
【題目】若各項均不為零的數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() ,
,![]() .
.
(1)證明數(shù)列![]() 是等比數(shù)列,并求
是等比數(shù)列,并求![]() 的通項公式;
的通項公式;
(2)設(shè)![]() ,是否存在正整數(shù)
,是否存在正整數(shù)![]() ,使得
,使得![]() 對于
對于![]() 恒成立.若存在,求出正整數(shù)
恒成立.若存在,求出正整數(shù)![]() 的最小值;若不存在,請說明理由.
的最小值;若不存在,請說明理由.
【答案】(1)證明詳見解析,![]() ;(2)存在,最小值為1.
;(2)存在,最小值為1.
【解析】
(1) ![]() ,①,得
,①,得![]() ,②,然后②-①得
,②,然后②-①得![]() ,③
,③
當(dāng)![]() 時,
時,![]() ,④, ③-④得
,④, ③-④得![]() ,驗證
,驗證![]() 時也成立,從而可證數(shù)列
時也成立,從而可證數(shù)列![]() 是等比數(shù)列,由定義可求得通項公式,
是等比數(shù)列,由定義可求得通項公式,
(2)求出![]() 后,利用裂項求和可求得
后,利用裂項求和可求得![]() ,再根據(jù)恒成立可求得
,再根據(jù)恒成立可求得![]() 的最小值.
的最小值.
![]() ,①,
,①,![]() ,②
,②
由數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() 及②-①得
及②-①得
![]() ,
,
![]() ,
,
![]() ,
,![]() ,③
,③
從而當(dāng)![]() 時,
時,![]() ,④
,④
③-④得![]() ,即
,即![]() ,所以
,所以![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() 令
令![]() ,得
,得![]() ,
,![]() ,
,![]() .
.
當(dāng)![]() 時,由
時,由![]() 得
得![]() ,
,
由![]() 知
知![]() ,此時
,此時![]() .
.
![]() 數(shù)列
數(shù)列![]() 是以
是以![]() 為首項,以
為首項,以![]() 為公比的等比數(shù)列,且
為公比的等比數(shù)列,且![]() .
.
(2)![]() ,
,
![]() ,
,
![]()
![]() .
.
假設(shè)存在正整數(shù)![]() ,使得
,使得![]() 對于
對于![]() 恒成立,
恒成立,
則![]() ,所以
,所以![]() 的最小值為1.
的最小值為1.


 海淀黃岡名師導(dǎo)航系列答案
海淀黃岡名師導(dǎo)航系列答案 普通高中同步練習(xí)冊系列答案
普通高中同步練習(xí)冊系列答案 優(yōu)翼小幫手同步口算系列答案
優(yōu)翼小幫手同步口算系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】在中國綠化基金會的支持下,庫布齊沙漠得到有效治理.2017年底沙漠的綠化率已達![]() ,從2018年開始,每年將出現(xiàn)這樣的情況,上一年底沙漠面積的
,從2018年開始,每年將出現(xiàn)這樣的情況,上一年底沙漠面積的![]() 被栽上樹改造為綠洲,而同時,上一年底綠洲面積的
被栽上樹改造為綠洲,而同時,上一年底綠洲面積的![]() 又被侵蝕,變?yōu)樯衬?/span>.
又被侵蝕,變?yōu)樯衬?/span>.
(1)設(shè)庫布齊沙漠面積為1,由綠洲面積和沙漠面積構(gòu)成.2017年底綠洲面積為![]() ,經(jīng)過1年綠洲面積為
,經(jīng)過1年綠洲面積為![]() ,經(jīng)過n年綠洲面積為
,經(jīng)過n年綠洲面積為![]() ,試用
,試用![]() 表示
表示![]() ;
;
(2)問至少需要經(jīng)過多少年的努力才能使庫布齊沙漠的綠洲面積超過![]() (年數(shù)取整數(shù)).
(年數(shù)取整數(shù)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】大城市往往人口密集,城市綠化在健康人民群眾肺方面發(fā)揮著非常重要的作用,歷史留給我們城市里的大山擁有品種繁多的綠色植物更是無價之寶.改革開放以來,有的地方領(lǐng)導(dǎo)片面追求政績,對森林資源野蠻開發(fā)受到嚴(yán)肅查處事件時有發(fā)生.2019年的春節(jié)后,廣西某市林業(yè)管理部門在“綠水青山就是金山銀山”理論的不斷指引下,積極從外地引進甲、乙兩種樹苗,并對甲、乙兩種樹苗各抽測了10株樹苗的高度(單位:厘米),數(shù)據(jù)如下面的莖葉圖:
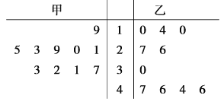
(1)據(jù)莖葉圖求甲、乙兩種樹苗的平均高度;
(2)據(jù)莖葉圖,運用統(tǒng)計學(xué)知識分析比較甲、乙兩種樹苗高度整齊情況.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 是平面內(nèi)兩個不共線的非零向量,
是平面內(nèi)兩個不共線的非零向量,![]() ,
,![]() ,
,![]() ,且
,且![]() 三點共線.
三點共線.
(1)求實數(shù)![]() 的值;
的值;
(2)已知![]() ,點
,點![]() ,若
,若![]() 四點按逆時針順序構(gòu)成平行四邊形,求點
四點按逆時針順序構(gòu)成平行四邊形,求點![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,內(nèi)角A、B、C的對邊分別為a、b、c,且滿足b2=ac,cosB=![]() .
.
(1)求![]() +
+![]() 的值;
的值;
(2)設(shè)![]()
![]() =
=![]() ,求三邊a、b、c的長度.
,求三邊a、b、c的長度.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形![]() 是邊長為2的菱形,且
是邊長為2的菱形,且![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,點
,點![]() 是線段
是線段![]() 上任意一點.
上任意一點.
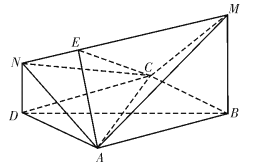
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 的最大值是
的最大值是![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】北京某附屬中學(xué)為了改善學(xué)生的住宿條件,決定在學(xué)校附近修建學(xué)生宿舍,學(xué)校總務(wù)辦公室用1000萬元從政府購得一塊廉價土地,該土地可以建造每層1000平方米的樓房,樓房的每平方米建筑費用與建筑高度有關(guān),樓房每升高一層,整層樓每平方米建筑費用提高![]() 萬元,已知建筑第5層樓房時,每平方米建筑費用為
萬元,已知建筑第5層樓房時,每平方米建筑費用為![]() 萬元.
萬元.
![]() 若學(xué)生宿舍建筑為x層樓時,該樓房綜合費用為y萬元,綜合費用是建筑費用與購地費用之和
若學(xué)生宿舍建筑為x層樓時,該樓房綜合費用為y萬元,綜合費用是建筑費用與購地費用之和![]() ,寫出
,寫出![]() 的表達式;
的表達式;
![]() 為了使該樓房每平方米的平均綜合費用最低,學(xué)校應(yīng)把樓層建成幾層?此時平均綜合費用為每平方米多少萬元?
為了使該樓房每平方米的平均綜合費用最低,學(xué)校應(yīng)把樓層建成幾層?此時平均綜合費用為每平方米多少萬元?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com