
【題目】如圖所示,在四邊形![]() 中:
中:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .點
.點![]() 為四邊形
為四邊形![]() 的外接圓劣弧
的外接圓劣弧![]() (不含
(不含![]() )上一動點.
)上一動點.

(1)證明:![]() ;
;
(2)若![]() ,設
,設![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)詳見解析;(2)![]() .
.
【解析】
(1)由余弦定理![]() 求得
求得![]() ,再根據
,再根據![]() ,求得
,求得![]() ,最后根據三邊長度判斷是否滿足勾股定理;
,最后根據三邊長度判斷是否滿足勾股定理;
(2)設![]() 交
交![]() 于
于![]() ,作
,作![]() 平行于
平行于![]() 且交
且交![]() 于
于![]() ,則四邊形
,則四邊形![]() 為平行四邊形,由平面向量基本定理和正弦定理表示
為平行四邊形,由平面向量基本定理和正弦定理表示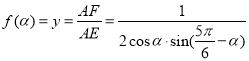 ,再根據三角恒等變形求
,再根據三角恒等變形求![]() 的最小值.
的最小值.
解:(1)在![]() 中,由余弦定理知:
中,由余弦定理知:
![]()
所以![]() ,又因為
,又因為![]() ,所以
,所以![]()
所以![]() 分別為方程
分別為方程![]() 的兩根,
的兩根,
因為![]() ,所以
,所以![]()
所以![]() ,所以
,所以![]()
(2)因為![]() ,所以
,所以![]() 是四邊形
是四邊形![]() 的外接圓的直徑,
的外接圓的直徑,![]()
所以四邊形![]() 為矩形,連接
為矩形,連接![]() ,
,![]()
設![]() 交
交![]() 于
于![]() ,作
,作![]() 平行于
平行于![]() 且交
且交![]() 于
于![]() ,則四邊形
,則四邊形![]() 為平行四邊形,
為平行四邊形,

所以![]() ,又因為
,又因為![]() ,
,
由平面向量基本定理知:![]() ,所以
,所以![]()
在![]() 中,因為
中,因為![]() ,
,![]() ,所以
,所以![]()
由正弦定理知:![]() ,所以
,所以![]()
在![]() 中,
中,![]()
所以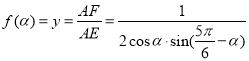 ,
,![]()
所以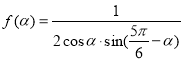
![]()
![]()
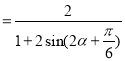
因為![]() ,所以
,所以![]() ,所以
,所以![]()
所以,當![]() 時,
時,![]() 取最小值,最小值為
取最小值,最小值為![]() .
.


科目:高中數學 來源: 題型:
【題目】在人群流量較大的街道,有一中年人吆喝“送錢”,只見他手拿一黑色小布袋,袋中有3只黃色、3只白色的乒乓球(其體積、質地完成相同),旁邊立著一塊小黑板寫道:
摸球方法:從袋中隨機摸出3個球,若摸得同一顏色的3個球,攤主送給摸球者5元錢;若摸得非同一顏色的3個球,摸球者付給攤主1元錢.
(1)摸出的3個球為白球的概率是多少?
(2)摸出的3個球為2個黃球1個白球的概率是多少?
(3)假定一天中有100人次摸獎,試從概率的角度估算一下這個攤主一個月(按30天計)能賺多少錢?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為
的定義域為![]() ,部分對應值如下表,
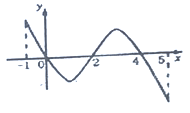
,部分對應值如下表,![]() 的導函數
的導函數![]() 的圖象如圖所示,給出關于
的圖象如圖所示,給出關于![]() 的下列命題:
的下列命題:
①函數![]() 在
在![]() 處取得極小值;
處取得極小值;
②函數![]() 在
在![]() 是減函數,在
是減函數,在![]() 是增函數;
是增函數;
③當![]() 時,函數
時,函數![]() 有4個零點;
有4個零點;
④如果當![]() 時,
時,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最小值為0.
的最小值為0.
其中所有的正確命題是__________(寫出正確命題的序號).

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩臺機床同時生產一種零件,在![]() 天中,兩臺機床每天生產的次品數分別為:
天中,兩臺機床每天生產的次品數分別為:
甲:![]() ;乙:
;乙:![]() .
.
(1)分別求兩組數據的眾數、中位數;
(2)根據兩組數據平均數和標準差的計算結果比較兩臺機床性能.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P-ABCD中,△PBC為正三角形,AB⊥平面PBC,AB∥CD,AB=![]() DC,
DC, ![]() .
.
(1)求證:AE∥平面PBC;
(2)求證:AE⊥平面PDC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學志愿者協會有![]() 名同學,成員構成如下表,其中表中部分數據不清楚,只知道從這
名同學,成員構成如下表,其中表中部分數據不清楚,只知道從這![]() 名同學中隨機抽取一位,抽到該名同學為“數學專業”的概率為
名同學中隨機抽取一位,抽到該名同學為“數學專業”的概率為![]() .
.
性別 專業 | 中文 | 英語 | 數學 | 體育 |
男 |
|
|
|
|
女 |
|
|
|
|
現從這![]() 名同學中隨機抽取
名同學中隨機抽取![]() 名同學參加社會公益活動(每位同學被選到的可能性相同).
名同學參加社會公益活動(每位同學被選到的可能性相同).
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求選出的![]() 名同學恰為專業互不相同的男生的概率
名同學恰為專業互不相同的男生的概率
(Ⅲ)設![]() 為選出的
為選出的![]() 名同學中“女生或數學專業”的學生的人數,求隨機變量
名同學中“女生或數學專業”的學生的人數,求隨機變量![]() 的分布列及其數學期望
的分布列及其數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}為遞增的等差數列,數列{bn}滿足bn=anan+1an+2(n∈N*),設Sn為數列{bn}的前n項和,若a2![]() ,則當Sn取得最小值時n的值為( )
,則當Sn取得最小值時n的值為( )
A.14B.13C.12D.11
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的離心率是
的離心率是![]() ,過點
,過點![]() 的動直線
的動直線![]() 于橢圓相交于
于橢圓相交于![]() 兩點,當直線
兩點,當直線![]() 平行于
平行于![]() 軸時,直線
軸時,直線![]() 被橢圓
被橢圓![]() 截得弦長為
截得弦長為![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)在![]() 上是否存在與點
上是否存在與點![]() 不同的定點
不同的定點![]() ,使得直線
,使得直線![]() 和
和![]() 的傾斜角互補?若存在,求
的傾斜角互補?若存在,求![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com