
【題目】確定函數![]() 的定義域、值域、單調區(qū)間、奇偶性、周期性.
的定義域、值域、單調區(qū)間、奇偶性、周期性.
【答案】定義域:![]() ;值域:
;值域:![]() ;單調區(qū)間:
;單調區(qū)間:![]() 的遞減區(qū)間是
的遞減區(qū)間是![]() ;遞增區(qū)間
;遞增區(qū)間![]() ;奇偶性:非奇非偶函數;周期性:周期函數,且最小正周期是
;奇偶性:非奇非偶函數;周期性:周期函數,且最小正周期是![]()
【解析】
化簡函數式為![]() ,根據對數函數的真數
,根據對數函數的真數![]() ,結合正弦函數的性質,可得
,結合正弦函數的性質,可得![]() 定義域;由正弦函數的有界性和對數函數的單調性,可得
定義域;由正弦函數的有界性和對數函數的單調性,可得![]() 的值域;利用復合函數單調性增減原則,結合正弦型函數的單調性,即可求出
的值域;利用復合函數單調性增減原則,結合正弦型函數的單調性,即可求出![]() 的單調性;先判斷定義域是否關于原點對稱,否則就是非奇非偶,若對稱,再判斷
的單調性;先判斷定義域是否關于原點對稱,否則就是非奇非偶,若對稱,再判斷![]() 與
與![]() 的關系;
的關系;![]() 的周期取決于
的周期取決于![]() 的周期.
的周期.
由已知![]() .
.
(1)欲使![]() 有意義,必須
有意義,必須![]() ,
,
![]() ,
,
即![]() ,
,
所以![]() 的定義域為
的定義域為![]() ;
;
(2)![]() ,
,
即![]() ,所以
,所以![]() 的值域為
的值域為![]() .
.
(3)考慮到![]() ,即
,即![]() .
.
當![]() ,即
,即![]() 時,
時,
![]() 單調遞增,
單調遞增,![]() 單調遞減,
單調遞減,
所以![]() 的遞減區(qū)間是
的遞減區(qū)間是![]() .
.
同理可求,![]() 的遞增區(qū)間
的遞增區(qū)間![]() .
.
(4)由于![]() 的定義域不關于原點對稱,所以
的定義域不關于原點對稱,所以![]() 是非奇非偶函數.
是非奇非偶函數.
(5)由于![]() 是周期為
是周期為![]() 的函數,
的函數,
所以![]() 是周期函數,且最小正周期是
是周期函數,且最小正周期是![]() .
.


 華東師大版一課一練系列答案
華東師大版一課一練系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數學 來源: 題型:
【題目】已知數列![]() 的各項均為正數,其前n項的積為
的各項均為正數,其前n項的積為![]() ,記
,記![]() ,
,![]() .
.
(1)若數列![]() 為等比數列,數列
為等比數列,數列![]() 為等差數列,求數列
為等差數列,求數列![]() 的公比.
的公比.
(2)若![]() ,
,![]() ,且
,且![]()
①求數列![]() 的通項公式.
的通項公式.
②記![]() ,那么數列
,那么數列![]() 中是否存在兩項
中是否存在兩項![]() ,(s,t均為正偶數,且
,(s,t均為正偶數,且![]() ),使得數列
),使得數列![]() ,
,![]() ,
,![]() ,成等差數列?若存在,求s,t的值;若不存在,請說明理由.
,成等差數列?若存在,求s,t的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )的焦距為4,其短軸的兩個端點與長軸的一個端點構成正三角形.
)的焦距為4,其短軸的兩個端點與長軸的一個端點構成正三角形.
(1)求橢圓C的標準方程;
(2)設F為橢圓C的左焦點,T為直線![]() 上任意一點,過F作TF的垂線交橢圓C于點P,Q.
上任意一點,過F作TF的垂線交橢圓C于點P,Q.
(i)證明:OT平分線段PQ(其中O為坐標原點);
(ii)當![]() 最小時,求點T的坐標.
最小時,求點T的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為棱
為棱![]() 上的點,且
上的點,且![]() .
.

(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)設![]() 為棱
為棱![]() 上的點(不與
上的點(不與![]() ,
,![]() 重合),且直線
重合),且直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某百貨商店今年春節(jié)期間舉行促銷活動,規(guī)定消費達到一定標準的顧客可進行一次抽獎活動,隨著抽獎活動的有效開展,參與抽獎活動的人數越來越多,該商店經理對春節(jié)前![]() 天參加抽獎活動的人數進行統計,
天參加抽獎活動的人數進行統計,![]() 表示第
表示第![]() 天參加抽獎活動的人數,得到統計表格如下:
天參加抽獎活動的人數,得到統計表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
(1)經過進一步統計分析,發(fā)現![]() 與
與![]() 具有線性相關關系.請根據上表提供的數據,用最小二乘法求出
具有線性相關關系.請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)該商店規(guī)定:若抽中“一等獎”,可領取600元購物券;抽中“二等獎”可領取300元購物券;抽中“謝謝惠顧”,則沒有購物券.已知一次抽獎活動獲得“一等獎”的概率為![]() ,獲得“二等獎”的概率為
,獲得“二等獎”的概率為![]() .現有張、王兩位先生參與了本次活動,且他們是否中獎相互獨立,求此二人所獲購物券總金額
.現有張、王兩位先生參與了本次活動,且他們是否中獎相互獨立,求此二人所獲購物券總金額![]() 的分布列及數學期望.
的分布列及數學期望.
參考公式: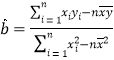 ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖甲所示的平面五邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,現將圖甲所示中的
,現將圖甲所示中的![]() 沿
沿![]() 邊折起,使平面
邊折起,使平面![]() 平面
平面![]() 得如圖乙所示的四棱錐
得如圖乙所示的四棱錐![]() .在如圖乙所示中
.在如圖乙所示中
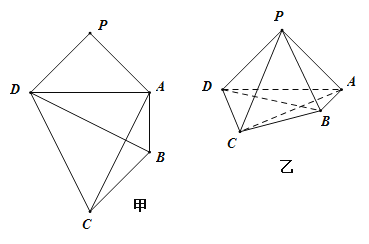
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)在棱![]() 上是否存在點
上是否存在點![]() 使得
使得![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() ?并說明理由.
?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在平面直角坐標系xOy中,曲線C的參數方程為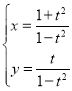 (t為參數).以原點O為極點,x軸正半軸為極軸建立極坐標系,直線l的極坐標方程為ρcos(
(t為參數).以原點O為極點,x軸正半軸為極軸建立極坐標系,直線l的極坐標方程為ρcos(![]() )
)![]() .
.
(1)求曲線C和直線l的直角坐標方程;
(2)若直線l交曲線C于A,B兩點,交x軸于點P,求![]() 的值.
的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com