
【題目】已知四棱錐![]() 中,底面ABCD是梯形,且
中,底面ABCD是梯形,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,AD的中點為E,則四棱錐
,AD的中點為E,則四棱錐![]() 外接球的表面積為________.
外接球的表面積為________.
 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案科目:高中數學 來源: 題型:
【題目】隨著經濟的發展,個人收入的提高,自2019年1月1日起,個人所得稅起征點和稅率作了調整.調整如下:納稅人的工資、薪金所得,以每月全部收入額減除5000元后的余額為應納稅所得額.依照個人所得稅稅率表,調整前后的計算方法如表:
個人所得稅稅率表 | 個人所得稅稅率表 | ||||
免征額3500元 | 免征額5000元 | ||||
級數 | 全月應納稅所得額 | 稅率 | 級數 | 全月應納稅所得額 | 稅率 |
1 | 不超過1500元部分 | 3 | 1 | 不超過3000元部分 | 3 |
2 | 超過1500元至4500元的部分 | 10 | 2 | 超過3000元至12000元的部分 | 10 |
3 | 超過4500元至9000元的部分 | 20 | 3 | 超過12000元至25000元的部分 | 20 |
|
|
|
|
|
|
(1)假如小明某月的工資、薪金等稅前收入為7500元,請你幫小明算一下調整后小明的實際收入比調整前增加了多少?
(2)某稅務部門在小明所在公司利用分層抽樣方法抽取某月100個不同層次員工的稅前收入,并制成下面的頻數分布表:
收入 |
|
|
|
|
|
|
人數 | 40 | 30 | 10 | 8 | 7 | 5 |
先從收入在![]() 及
及![]() 的人群中按分層抽樣抽取7人,再從中選3人作為新納稅法知識宣講員,用隨機變量X表示抽到作為宣講員的收入在
的人群中按分層抽樣抽取7人,再從中選3人作為新納稅法知識宣講員,用隨機變量X表示抽到作為宣講員的收入在![]() 元的人數,求X的分布列與數學期望.
元的人數,求X的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓M:(x+m)2+y2=4n2(m,n>0且m≠n),點N(m,0),P是圓M上的動點,線段PN的垂直平分線交直線PM于點Q,點Q的軌跡為曲線C.
(1)討論曲線C的形狀,并求其方程;
(2)若m=1,且△QMN面積的最大值為![]() .直線l過點N且不垂直于坐標軸,l與曲線C交于A,B,點B關于x軸的對稱點為D.求證:直線AD過定點,并求出該定點的坐標.
.直線l過點N且不垂直于坐標軸,l與曲線C交于A,B,點B關于x軸的對稱點為D.求證:直線AD過定點,并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】1852年,英國來華傳教士偉烈亞力將《孫子算經》中“物不知數”問題的解法傳至歐洲.1874年,英國數學家馬西森指出此法符合1801年由高斯得到的關于同余式解法的一般性定理,因而西方稱之為“中國剩余定理”.“中國剩余定理”講的是一個關于整除的問題,例如求1到2000這2000個整數中,能被3除余1且被7除余1的數的個數,現由程序框圖,其中MOD函數是一個求余函數,記![]() 表示m除以n的余數,例如
表示m除以n的余數,例如![]() ,則輸出i為( ).
,則輸出i為( ).
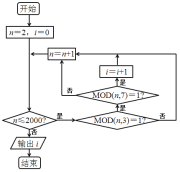
A.98B.97C.96D.95
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了普及環保知識,增強環保意識,某大學從理工類專業的![]() 班和文史類專業的
班和文史類專業的![]() 班各抽取
班各抽取![]() 名同學參加環保知識測試,統計得到成績與專業的列聯表:( )
名同學參加環保知識測試,統計得到成績與專業的列聯表:( )
優秀 | 非優秀 | 總計 | |
| 14 | 6 | 20 |
| 7 | 13 | 20 |
總計 | 21 | 19 | 40 |
附:參考公式及數據:
(1)統計量:![]() ,(
,(![]() ).
).
(2)獨立性檢驗的臨界值表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
則下列說法正確的是
A. 有![]() 的把握認為環保知識測試成績與專業有關
的把握認為環保知識測試成績與專業有關
B. 有![]() 的把握認為環保知識測試成績與專業無關
的把握認為環保知識測試成績與專業無關
C. 有![]() 的把握認為環保知識測試成績與專業有關
的把握認為環保知識測試成績與專業有關
D. 有![]() 的把握認為環保知識測試成績與專業無關
的把握認為環保知識測試成績與專業無關
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,拋物線
,拋物線![]() 與圓
與圓![]() 的相交弦長為4.
的相交弦長為4.
(1)求拋物線![]() 的標準方程;
的標準方程;
(2)點![]() 為拋物線
為拋物線![]() 的焦點,
的焦點,![]() 為拋物線
為拋物線![]() 上兩點,
上兩點,![]() ,若
,若![]() 的面積為
的面積為![]() ,且直線
,且直線![]() 的斜率存在,求直線
的斜率存在,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中正確的是( )
A.若p∨q為真命題,則p∧q為真命題
B.“x=5”是“x2-4x-5=0”的充分不必要條件
C.命題“若x<-1,則x2-2x-3>0”的否定為:“若x≥-1,則x2-2x-3≤0”
D.已知命題p:x∈R,x2+x-1<0,則![]() p:x∈R,x2+x-1≥0
p:x∈R,x2+x-1≥0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com