【題目】已知雙曲線
的左、右焦點分別為
，實軸長為4，漸近線方程為
，點N在圓
上，則
的最小值為( )
A. 
B. 5C. 6D. 7
【答案】B
【解析】
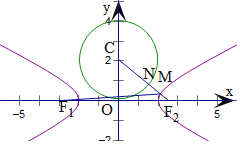
求得雙曲線的a，b，可得雙曲線方程，求得焦點坐標，運用雙曲線的定義和三點共線取得最小值，連接CF2，交雙曲線于M，圓于N，計算可得所求最小值．
由題意可得2a＝4，即a＝2，
漸近線方程為y＝±
x，即有
，
即b＝1，可得雙曲線方程為
y2＝1，
焦點為F1（
，0），F2，（
，0），
由雙曲線的定義可得|MF1|＝2a+|MF2|＝4+|MF2|，
由圓x2+y2﹣4y＝0可得圓心C（0，2），半徑r＝2，
|MN|+|MF1|＝4+|MN|+|MF2|，
連接CF2，交雙曲線于M，圓于N，
可得|MN|+|MF2|取得最小值，且為|CF2|
3，
則則|MN|+|MF1|的最小值為4+3﹣2＝5．
故選：B．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】空氣質量指數PM2.5（單位：μg/m3）表示每立方米空氣中可入肺顆粒物的含量，這個值越高，就代表空氣污染越嚴重：
日均濃度 |
|
|
|
|
|
|
空氣質量級別 | 一級 | 二級 | 三級 | 四級 | 五級 | 六級 |
空氣質量類型 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
甲、乙兩城市2013年2月份中的15天對空氣質量指數PM2.5進行監測，獲得PM2.5日均濃度指數數據如莖葉圖所示：
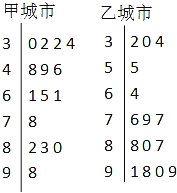
（Ⅰ）根據你所學的統計知識估計甲、乙兩城市15天內哪個城市空氣質量總體較好？（注：不需說明理由）
（Ⅱ）在15天內任取1天，估計甲、乙兩城市空氣質量類別均為優或良的概率；
（Ⅲ）在乙城市15個監測數據中任取2個，設X為空氣質量類別為優或良的天數，求X的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】裴波那契數列（Fibonacci sequence ）又稱黃金分割數列，因為數學家列昂納多·裴波那契以兔子繁殖為例子引入，故又稱為“兔子數列”，在數學上裴波那契數列被以下遞推方法定義：數列
滿足：
，
，現從該數列的前40項中隨機抽取一項，則能被3整除的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在發生某公共衛生事件期間，有專業機構認為該事件在一段時間內沒有發生大規模群體感染的標志是“連續10日，每天新增疑似病例不超過7人”.過去10日，甲、乙、丙、丁四地新增疑似病例數據信息如下：
甲地：總體平均數為3，中位數為4；
乙地：總體平均數為1，總體方差大于0；
丙地：總體平均數為2，總體方差為3；
丁地：中位數為2，眾數為3；
則甲、乙、兩、丁四地中，一定沒有發生大規模群體感染的是（ ）
A.甲地B.乙地C.丙地D.丁地
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】中醫藥，是包括漢族和少數民族醫藥在內的我國各民族醫藥的統稱，是反映中華民族對生命、健康和疾病的認識，具有悠久歷史傳統和獨特理論及技術方法的醫藥學體系，是中華民族的瑰寶.某科研機構研究發現，某品種中醫藥的藥物成分甲的含量
（單位：克）與藥物功效
（單位：藥物單位）之間具有關系
.檢測這種藥品一個批次的5個樣本，得到成分甲的平均值為4克，標準差為
克，則估計這批中醫藥的藥物功效的平均值為（ ）
A.22藥物單位B.20藥物單位C.12藥物單位D.10藥物單位
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列{an}滿足：a1=
，a2=
，且a1a2+a2a3+…+anan+1=na1an+1對任何的正整數n都成立，則
的值為（ ）
A. 5032 B. 5044 C. 5048 D. 5050
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解某地區初中學生的體質健康情況,統計了該地區8所學校學生的體質健康數據,按總分評定等級為優秀,良好,及格,不及格.良好及其以上的比例之和超過40%的學校為先進校.各等級學生人數占該校學生總人數的比例如下表:
比例 學校 等級 | 學校A | 學校B | 學校C | 學校D | 學校E | 學校F | 學校G | 學校H |
優秀 | 8% | 3% | 2% | 9% | 1% | 22% | 2% | 3% |
良好 | 37% | 50% | 23% | 30% | 45% | 46% | 37% | 35% |
及格 | 22% | 30% | 33% | 26% | 22% | 17% | 23% | 38% |
不及格 | 33% | 17% | 42% | 35% | 32% | 15% | 38% | 24% |
(1)從8所學校中隨機選出一所學校,求該校為先進校的概率；
(2)從8所學校中隨機選出兩所學校,記這兩所學校中不及格比例低于30%的學校個數為X,求X的分布列；
(3)設8所學校優秀比例的方差為S12,良好及其以下比例之和的方差為S22,比較S12與S22的大小.(只寫出結果)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列{an}的前n項和為Sn，且Sn＝n(n+1)(n∈N*).
(1)求數列{an}的通項公式；
(2)若數列{bn}滿足：
，求數列{bn}的通項公式；
(3)令
(n∈N*)，求數列{cn}的前n項和Tn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
