
【題目】已知橢圓![]() :
:![]() 的左右焦點分別為
的左右焦點分別為![]() 、
、![]() ,左右頂點分別是
,左右頂點分別是![]() 、
、![]() ,長軸長為
,長軸長為![]() ,
,![]() 是以原點為圓心,
是以原點為圓心,![]() 為半徑的圓的任一條直徑,四邊形
為半徑的圓的任一條直徑,四邊形![]() 的面積最大值為
的面積最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)不經過原點的直線![]() :
:![]() 與橢圓交于
與橢圓交于![]() 、
、![]() 兩點,
兩點,
①若直線![]() 與
與![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,且
,且![]() ,求證:直線
,求證:直線![]() 過定點,并求出該定點的坐標;
過定點,并求出該定點的坐標;
②若直線![]() 的斜率是直線
的斜率是直線![]() 、
、![]() 斜率的等比中項,求
斜率的等比中項,求![]() 面積的取值范圍.
面積的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由題可得![]() ,再由四邊形
,再由四邊形![]() 的面積最大值為
的面積最大值為![]() 列方程即可求得
列方程即可求得![]() ,問題得解。
,問題得解。
(2)①設![]() ,
,![]() ,聯立直線與橢圓方程可得:
,聯立直線與橢圓方程可得:![]() ,即可表示出
,即可表示出![]() ,
,![]() ,再整理
,再整理![]() ,可得:
,可得:![]() ,問題得解。
,問題得解。
②由直線![]() 的斜率是直線
的斜率是直線![]() 、
、![]() 斜率的等比中項即可求得
斜率的等比中項即可求得![]() ,再由弦長公式求得
,再由弦長公式求得![]() ,求出點
,求出點![]() 到直線
到直線![]() 的距離
的距離![]() ,即可表示
,即可表示![]() ,再利用基本不等式即可得解。
,再利用基本不等式即可得解。
(1)由題可得:![]() ,即:
,即:![]() ,
,
當![]() 與
與![]() 軸重合時,四邊形
軸重合時,四邊形![]() 的面積最大值
的面積最大值
由已知可得:![]() ,解得:
,解得:![]()
所以橢圓方程為:![]() .
.
(2)①證明:設![]() ,
,![]() ,
,
將![]() 代入橢圓方程得:
代入橢圓方程得:![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴直線![]() 的方程為
的方程為![]() ,即
,即![]() ,
,
故直線![]() 恒過定點
恒過定點![]() ;
;
②由直線![]() 的斜率是直線
的斜率是直線![]() ,
,![]() 斜率的等比中項,
斜率的等比中項,
即有![]() ,即
,即![]() ,
,
∴![]() ,整理得:
,整理得:![]() ,解得
,解得![]() ,
,
代入![]() 有
有![]() ,
,
![]() ,
,
點![]() 到直線
到直線![]() 的距離
的距離![]() ,
,
∴![]()
![]() ,
,
(當且僅當![]() 時,等號成立)
時,等號成立)
所以![]() 面積的取值范圍是:
面積的取值范圍是:![]() .
.


科目:高中數學 來源: 題型:
【題目】司機在開機動車時使用手機是違法行為,會存在嚴重的安全隱患,危及自己和他人的生命. 為了研究司機開車時使用手機的情況,交警部門調查了![]() 名機動車司機,得到以下統計:在
名機動車司機,得到以下統計:在![]() 名男性司機中,開車時使用手機的有
名男性司機中,開車時使用手機的有![]() 人,開車時不使用手機的有
人,開車時不使用手機的有![]() 人;在
人;在![]() 名女性司機中,開車時使用手機的有
名女性司機中,開車時使用手機的有![]() 人,開車時不使用手機的有
人,開車時不使用手機的有![]() 人.
人.
(1)完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為開車時使用手機與司機的性別有關;
的把握認為開車時使用手機與司機的性別有關;
開車時使用手機 | 開車時不使用手機 | 合計 | |
男性司機人數 | |||
女性司機人數 | |||
合計 |
(2)以上述的樣本數據來估計總體,現交警部門從道路上行駛的大量機動車中隨機抽檢3輛,記這3輛車中司機為男性且開車時使用手機的車輛數為![]() ,若每次抽檢的結果都相互獨立,求
,若每次抽檢的結果都相互獨立,求![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
參考公式與數據:
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式
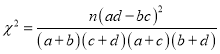 span>,其中
span>,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:![]() 經過點
經過點![]() ,A,B是拋物線C上異于點O的不同的兩點,其中O為原點.
,A,B是拋物線C上異于點O的不同的兩點,其中O為原點.
(1)求拋物線C的方程,并求其焦點坐標和準線方程;
(2)若![]() ,求
,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
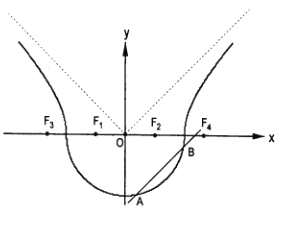
【題目】如圖,曲線![]() 由曲線
由曲線![]() 和曲線
和曲線![]() 組成,其中點
組成,其中點![]() 為曲線
為曲線![]() 所在圓錐曲線的焦點,點
所在圓錐曲線的焦點,點![]() 為曲線
為曲線![]() 所在圓錐曲線的焦點.
所在圓錐曲線的焦點.
(1)若![]() ,求曲線
,求曲線![]() 的方程;
的方程;
(2)如圖,作直線![]() 平行于曲線
平行于曲線![]() 的漸近線,交曲線
的漸近線,交曲線![]() 于點
于點![]() ,求證:弦
,求證:弦![]() 的中點
的中點![]() 必在曲線
必在曲線![]() 的另一條漸近線上;
的另一條漸近線上;
(3)對于(1)中的曲線![]() ,若直線
,若直線![]() 過點
過點![]() 交曲線
交曲線![]() 于點
于點![]() ,求
,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2+2x-4y+3=0.
(1)若圓C的切線在x軸和y軸上的截距相等,求此切線的方程.
(2)從圓C外一點P(x1,y1)向該圓引一條切線,切點為M,O為坐標原點,且有|PM|=|PO|,求使得|PM|取得最小值的點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,短軸長為2;
,短軸長為2;
(1)求橢圓的標準方程;
(2)設橢圓上頂點![]() ,左、右頂點分別為
,左、右頂點分別為![]() 、
、![]() .直線
.直線![]() 且交橢圓于
且交橢圓于![]() 、
、![]() 兩點,點E 關于
兩點,點E 關于![]() 軸的對稱點為點
軸的對稱點為點![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在五棱錐P-ABCDE中,△ABE是等邊三角形,四邊形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中點,點P在底面的射影落在線段AG上.
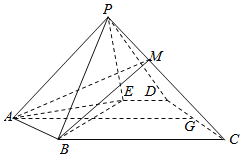
(Ⅰ)求證:平面PBE⊥平面APG;
(Ⅱ)已知AB=2,BC=![]() ,側棱PA與底面ABCDE所成角為45°,S△PBE=
,側棱PA與底面ABCDE所成角為45°,S△PBE=![]() ,點M在側棱PC上,CM=2MP,求二面角M-AB-D的余弦值.
,點M在側棱PC上,CM=2MP,求二面角M-AB-D的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com