
【題目】某同學用“五點法”畫函數f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一周期內的圖象時,列表并填入了部分數據,如下表:
)在某一周期內的圖象時,列表并填入了部分數據,如下表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 3 | 0 |
(1)請將上表空格中的數據在答卷的相應位置上,并求函數f(x)的解析式;
(2)若y=f(x)的圖象上所有點向左平移 ![]() 個單位后對應的函數為g(x),求當x∈[﹣
個單位后對應的函數為g(x),求當x∈[﹣ ![]() ,
, ![]() ]時,函數y=g(x)的值域.
]時,函數y=g(x)的值域.
【答案】
(1)解:由題意可得,A=3, ![]()
![]() =
= ![]() ﹣
﹣ ![]() ,ω=2,
,ω=2,
再根據五點法作圖可得2 ![]() +φ=
+φ= ![]() ,求得φ=﹣
,求得φ=﹣ ![]() ,∴f(x)=3sin(2x﹣
,∴f(x)=3sin(2x﹣ ![]() ).
).
表格即:
2x﹣ | 0 |
| π |
| 2π |
x |
|
|
|
|
|
3sin(2x﹣ | 0 | 3 | 0 | ﹣3 | 0 |
(2)解:把y=f(x)的圖象上所有點向左平移 ![]() 個單位后對應的函數為g(x)=3sin[2(x+
個單位后對應的函數為g(x)=3sin[2(x+ ![]() )﹣
)﹣ ![]() ]
]
=3sin(2x+ ![]() ),
),
當x∈[﹣ ![]() ,
, ![]() ]時,2x+
]時,2x+ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],sin(2x+
],sin(2x+ ![]() )∈[﹣
)∈[﹣ ![]() ,1],
,1],
∴3sin(2x+ ![]() )∈[﹣
)∈[﹣ ![]() ,3],即函數y=g(x)的值域為[﹣
,3],即函數y=g(x)的值域為[﹣ ![]() ,3]
,3]
【解析】(1)由函數的最值求出A,由周期求出ω,由五點法作圖求出φ的值,可得函數的解析式.(2)利用y=Asin(ωx+φ)的圖象變換規律求得g(x)的解析式,再利用正弦函數的定義域和值域求得函數y=g(x)的值域.
【考點精析】關于本題考查的函數y=Asin(ωx+φ)的圖象變換,需要了解圖象上所有點向左(右)平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數
倍(橫坐標不變),得到函數![]() 的圖象才能得出正確答案.
的圖象才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】數列{an}中,a1=1,an+an+1=( ![]() )n , Sn=a1+4a2+42a3+…+4n﹣1an , 類比課本中推導等比數列前項和公式的方法,可求得5Sn﹣4nan= .
)n , Sn=a1+4a2+42a3+…+4n﹣1an , 類比課本中推導等比數列前項和公式的方法,可求得5Sn﹣4nan= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,游客從某旅游景區的景點A處下山至C處有兩種路徑.一種是從A沿直線步行到C,另一種是先從A沿索道乘纜車到B,然后從B沿直線步行到C.現有甲、乙兩位游客從A處下山,甲沿AC勻速步行,速度為50m/min.在甲出發2min后,乙從A乘纜車到B,在B處停留1min后,再從B勻速步行到C.假設纜車勻速直線運動的速度為130m/min,山路AC長為1260m,經測量,cosA= ![]() ,cosC=
,cosC= ![]()
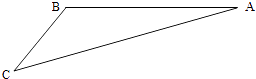
(1)求索道AB的長;
(2)問乙出發多少分鐘后,乙在纜車上與甲的距離最短?
(3)為使兩位游客在C處互相等待的時間不超過3分鐘,乙步行的速度應控制在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=3sin(2x+ ![]() )的圖象為C,關于函數f(x)及其圖象的判斷如下: ①圖象C關于點(
)的圖象為C,關于函數f(x)及其圖象的判斷如下: ①圖象C關于點( ![]() ,0)對稱;
,0)對稱;
②圖象C關于直線x= ![]() 對稱;
對稱;
③由圖象C向右平移 ![]() 個單位長度可以得到y=3sin2x的圖象;
個單位長度可以得到y=3sin2x的圖象;
④函數f(x)在區間(﹣ ![]() ,
, ![]() )內是減函數;
)內是減函數;
⑤函數|f(x)+1|的最小正周期為 ![]() .
.
其中正確的結論序號是 . (把你認為正確的結論序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() ,向量
,向量![]() ,函數
,函數![]() .
.
(1)求![]() 的單調減區間;
的單調減區間;
(2)將函數![]() 圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再把得到的圖象向左平移
圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再把得到的圖象向左平移![]() 個單位長度,得到
個單位長度,得到![]() 的圖象,求函數
的圖象,求函數![]() 的解析式及其圖象的對稱中心.
的解析式及其圖象的對稱中心.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 經過不同的三點
經過不同的三點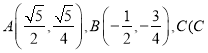 在第三象限),線段
在第三象限),線段![]() 的中點在直線
的中點在直線![]() 上.
上.
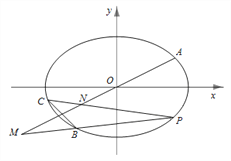
(Ⅰ)求橢圓![]() 的方程及點
的方程及點![]() 的坐標;
的坐標;
(Ⅱ)設點![]() 是橢圓
是橢圓![]() 上的動點(異于點
上的動點(異于點![]() 且直線
且直線![]() 分別交直線
分別交直線![]() 于
于![]() 兩點,問
兩點,問![]() 是否為定值?若是,求出定值;若不是,請說明理由.
是否為定值?若是,求出定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4![]() 4:坐標系與參數方程
4:坐標系與參數方程
在平面直角坐標系![]() 中,圓C的參數方程為
中,圓C的參數方程為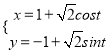 ,(t為參數),在以原點O為極點,x軸的非負半軸為極軸建立的極坐標系中,直線
,(t為參數),在以原點O為極點,x軸的非負半軸為極軸建立的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() ,A,B兩點的極坐標分別為
,A,B兩點的極坐標分別為![]() .
.
(Ⅰ)求圓C的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)點P是圓C上任一點,求△PAB面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 分別為雙曲線
分別為雙曲線![]() 的左、右頂點,雙曲線的實軸長為
的左、右頂點,雙曲線的實軸長為![]() ,焦點到漸近線的距離為
,焦點到漸近線的距離為![]() .
.
(1)求雙曲線的方程;
(2)已知直線![]() 與雙曲線的右支交于
與雙曲線的右支交于![]() 兩點,且在雙曲線的右支上存在點
兩點,且在雙曲線的右支上存在點![]() ,使
,使![]() ,求
,求![]() 的值及點
的值及點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com