
【題目】已知函數(shù)![]() =lnx+ax2+(2a+1)x.
=lnx+ax2+(2a+1)x.
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)a﹤0時(shí),證明![]() .
.
【答案】(1)見(jiàn)解析;(2)見(jiàn)解析.
【解析】試題分析:(1)先求函數(shù)導(dǎo)數(shù)![]() ,再根據(jù)導(dǎo)函數(shù)符號(hào)的變化情況討論單調(diào)性:當(dāng)
,再根據(jù)導(dǎo)函數(shù)符號(hào)的變化情況討論單調(diào)性:當(dāng)![]() 時(shí),
時(shí), ![]() ,則
,則![]() 在
在![]() 單調(diào)遞增;當(dāng)
單調(diào)遞增;當(dāng)![]() 時(shí),
時(shí), ![]() 在
在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減.(2)證明
單調(diào)遞減.(2)證明![]() ,即證
,即證![]() ,而
,而![]() ,所以需證
,所以需證![]() ,設(shè)g(x)=lnx-x+1 ,利用導(dǎo)數(shù)易得
,設(shè)g(x)=lnx-x+1 ,利用導(dǎo)數(shù)易得![]() ,即得證.
,即得證.
試題解析:(1)f(x)的定義域?yàn)椋?,+![]() ),
),![]() .
.
若a≥0,則當(dāng)x∈(0,+![]() )時(shí),
)時(shí), ![]() ,故f(x)在(0,+
,故f(x)在(0,+![]() )單調(diào)遞增.
)單調(diào)遞增.
若a<0,則當(dāng)x∈![]() 時(shí),
時(shí), ![]() ;當(dāng)x∈
;當(dāng)x∈![]() 時(shí),
時(shí), ![]() .故f(x)在
.故f(x)在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減.
單調(diào)遞減.
(2)由(1)知,當(dāng)a<0時(shí),f(x)在![]() 取得最大值,最大值為
取得最大值,最大值為
![]() .
.
所以![]() 等價(jià)于
等價(jià)于![]() ,即
,即![]() .
.
設(shè)g(x)=lnx-x+1,則![]() .
.
當(dāng)x∈(0,1)時(shí), ![]() ;當(dāng)x∈(1,+
;當(dāng)x∈(1,+![]() )時(shí),
)時(shí), ![]() .所以g(x)在(0,1)單調(diào)遞增,在(1,+
.所以g(x)在(0,1)單調(diào)遞增,在(1,+![]() )單調(diào)遞減.故當(dāng)x=1時(shí),g(x)取得最大值,最大值為g(1)=0.所以當(dāng)x>0時(shí),g(x)≤0.從而當(dāng)a<0時(shí),
)單調(diào)遞減.故當(dāng)x=1時(shí),g(x)取得最大值,最大值為g(1)=0.所以當(dāng)x>0時(shí),g(x)≤0.從而當(dāng)a<0時(shí), ![]() ,即
,即![]() .
.


 名師伴你成長(zhǎng)課時(shí)同步學(xué)練測(cè)系列答案
名師伴你成長(zhǎng)課時(shí)同步學(xué)練測(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】【2017安徽淮北二模】選修4—4:坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系![]() 中, 以
中, 以![]() 為極點(diǎn),
為極點(diǎn), ![]() 軸正半軸為極軸建立極坐標(biāo)系, 圓
軸正半軸為極軸建立極坐標(biāo)系, 圓![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,直線
,直線![]() 的參數(shù)方程為
的參數(shù)方程為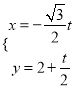 (t為參數(shù)), 直線
(t為參數(shù)), 直線![]() 和圓
和圓![]() 交于
交于![]() 兩點(diǎn)。
兩點(diǎn)。
(Ⅰ)求圓心的極坐標(biāo);
(Ⅱ)直線![]() 與
與![]() 軸的交點(diǎn)為
軸的交點(diǎn)為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】[選修4-4:坐標(biāo)系與參數(shù)方程]在平面坐標(biāo)系中xOy中,已知直線l的參考方程為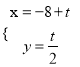 (t為參數(shù)),曲線C的參數(shù)方程為
(t為參數(shù)),曲線C的參數(shù)方程為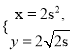 (s為參數(shù))。設(shè)p為曲線C上的動(dòng)點(diǎn),求點(diǎn)P到直線l的距離的最小值
(s為參數(shù))。設(shè)p為曲線C上的動(dòng)點(diǎn),求點(diǎn)P到直線l的距離的最小值
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】一元二次不等式ax2+bx+c>0的解集是(﹣ ![]() ,2),則cx2+bx+a<0的解集是( )
,2),則cx2+bx+a<0的解集是( )
A.(﹣3, ![]() )
)
B.(﹣∞,﹣3)∪( ![]() ,+∞)
,+∞)
C.(﹣2, ![]() )
)
D.(﹣∞,﹣2)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】三棱柱ABC﹣A1B1C1的側(cè)面AA1C1C為正方形,側(cè)面AA1B1B⊥側(cè)面BB1C1C,且AC=2,AB= ![]() ,∠A1AB=45°,E、F分別為AA1、CC1的中點(diǎn).
,∠A1AB=45°,E、F分別為AA1、CC1的中點(diǎn). 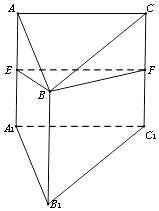
(1)求證:AA1⊥平面BEF;
(2)求二面角B﹣EB1﹣C1的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】給出下列命題:
(1)函數(shù)y=tanx在定義域內(nèi)單調(diào)遞增;
(2)若α,β是銳角△ABC的內(nèi)角,則sinα>cosβ;
(3)函數(shù)y=cos( ![]() x+
x+ ![]() )的對(duì)稱(chēng)軸x=
)的對(duì)稱(chēng)軸x= ![]() +kπ,k∈Z;
+kπ,k∈Z;
(4)函數(shù)y=sin2x的圖象向左平移 ![]() 個(gè)單位,得到y(tǒng)=sin(2x+
個(gè)單位,得到y(tǒng)=sin(2x+ ![]() )的圖象.
)的圖象.
其中正確的命題的序號(hào)是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)橢圓![]() :
: ![]() (
(![]() )的左右焦點(diǎn)分別為
)的左右焦點(diǎn)分別為![]() ,
, ![]() ,下頂點(diǎn)為
,下頂點(diǎn)為![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
(Ⅰ)求橢圓![]() 的離心率;
的離心率;
(Ⅱ)設(shè)![]() 為橢圓上異于其頂點(diǎn)的一點(diǎn),
為橢圓上異于其頂點(diǎn)的一點(diǎn), ![]() 到直線
到直線![]() 的距離為
的距離為![]() ,且三角形
,且三角形![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相切,過(guò)焦點(diǎn)
相切,過(guò)焦點(diǎn)![]() ,
, ![]() 分別作
分別作![]() ,
, ![]() ,垂足分別為
,垂足分別為![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】通過(guò)隨機(jī)詢(xún)問(wèn)110名性別不同的行人,對(duì)過(guò)馬路是愿意走斑馬線還是愿意走人行天橋進(jìn)行抽樣調(diào)查,得到如下的列聯(lián)表:
男 | 女 | 總計(jì) | |
走天橋 | 40 | 20 | 60 |
走斑馬線 | 20 | 30 | 50 |
總計(jì) | 60 | 50 | 110 |
由 ![]() ,算得
,算得 ![]()
參照獨(dú)立性檢驗(yàn)附表,得到的正確結(jié)論是( )
A.有99%的把握認(rèn)為“選擇過(guò)馬路的方式與性別有關(guān)”
B.有99%的把握認(rèn)為“選擇過(guò)馬路的方式與性別無(wú)關(guān)”
C.在犯錯(cuò)誤的概率不超過(guò)0.1%的前提下,認(rèn)為“選擇過(guò)馬路的方式與性別有關(guān)”
D.在犯錯(cuò)誤的概率不超過(guò)0.1%的前提下,認(rèn)為“選擇過(guò)馬路的方式與性別無(wú)關(guān)”
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)f(x)=cos(ωx+φ)(ω>0,﹣ ![]() <φ<0)的最小正周期為π,且f(
<φ<0)的最小正周期為π,且f( ![]() )=
)= ![]() .
. 
(1)求ω和φ的值;
(2)在給定坐標(biāo)系中作出函數(shù)f(x)在[0,π]上的圖象.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com