Question

設F₁，F₂分別為雙曲線

x2

a2

-

y2

b2

=1（a＞0，b＞0）的左、右焦點，過F₂的直線交雙曲線的右支于A，B兩點，設△AF₁F₂和△BF₁F₂的內心分別為C，D，若當|CD|=

9a

4

時，直線的傾斜角的正弦為

8

9

．則雙曲線的離心率為

 

．

Answer 1

考點：雙曲線的簡單性質

專題：計算題,直線與圓,圓錐曲線的定義、性質與方程

分析：充分利用平面幾何圖形的性質解題．因從同一點出發的切線長相等，得|AM|=|AN|，|F₁M|=|F₁E|，|F₂N|=|F₂E|，再結合雙曲線的定義得|F₁E|-|F₂E|=2a，從而即可求得△AF₁F₂的內心的橫坐標a，即有CD⊥x軸，在△CF₂D中，運用解直角三角形知識，可得|CD|=（c-a）（tan

θ

2

+tan（90°-

θ

2

））=

9a

4

，運用切化弦和二倍角公式化簡即可得到離心率．

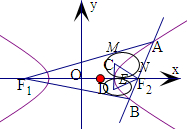
解答： 解：記△AF₁F₂的內切圓圓心為C，
邊AF₁、AF₂、F₁F₂上的切點分別為M、N、E，
易見C、E橫坐標相等，則|AM|=|AN|，|F₁M|=|F₁E|，|F₂N|=|F₂E|，
由|AF₁|-|AF₂|=2a，
即|AM|+|MF₁|-（|AN|+|NF₂|）=2a，得|MF₁|-|NF₂|=2a，
即|F₁E|-|F₂E|=2a，記C的橫坐標為x₀，則E（x₀，0），
于是x₀+c-（c-x₀）=2a，得x₀=a，
同樣內心D的橫坐標也為a，則有CD⊥x軸，
由直線的傾斜角θ的正弦為

8

9

，則∠OF₂D=

θ

2

，∠CF₂O=90°-

θ

2

，
在△CF₂D中，|CD|=（c-a）（tan

θ

2

+tan（90°-

θ

2

））=（c-a）•

1+tan2 θ 2

tan θ 2

=（c-a）•

cos2 θ 2 +sin2 θ 2

sin θ 2 cos θ 2

=

2

sinθ

•（c-a）=

2

8 9

•（c-a）=

9a

4

，
則c-a=a，即c=2a，
即有e=

c

a

=2．
故答案為：2．

點評：本題考查雙曲線的定義、方程和性質，考查三角形的內心的概念，考查三角函數的化簡和求值，考察離心率的求法，屬于中檔題．