
【題目】已知函數(shù)![]() ,其中
,其中![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,且對任意的
,且對任意的![]() ,都有
,都有![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() ,
,![]() ,且
,且![]() 在
在![]() 單調(diào)遞增,求
單調(diào)遞增,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)代入![]() ,
,![]() 可求得
可求得![]() 的解析式.代入不等式化簡,將不等式化簡為關(guān)于
的解析式.代入不等式化簡,將不等式化簡為關(guān)于![]() 的二次函數(shù)形式,結(jié)合
的二次函數(shù)形式,結(jié)合![]() 即可求得
即可求得![]() 的取值范圍.
的取值范圍.
(2)解法1:根據(jù)條件![]() 可求得函數(shù)
可求得函數(shù)![]() 的對稱軸,且由
的對稱軸,且由![]() 可得
可得![]() 的表達(dá)式.再根據(jù)
的表達(dá)式.再根據(jù)![]() 在
在![]() 單調(diào)遞增,可得關(guān)于
單調(diào)遞增,可得關(guān)于![]() 的不等式組,解不等式組即可求得
的不等式組,解不等式組即可求得![]() 的最大值.
的最大值.
解法2:根據(jù)![]() 在
在![]() 單調(diào)遞增可先求得
單調(diào)遞增可先求得![]() 的取值范圍,結(jié)合
的取值范圍,結(jié)合![]() 可得函數(shù)
可得函數(shù)![]() 的對稱軸, 且由
的對稱軸, 且由![]() 可得
可得![]() 的表達(dá)式.根據(jù)
的表達(dá)式.根據(jù)![]() 可求得
可求得![]() 的值,再求得于
的值,再求得于![]() 的值,即可得
的值,即可得![]() 的解析式.進(jìn)而求得滿足
的解析式.進(jìn)而求得滿足![]() 在
在![]() 單調(diào)遞增時(shí)
單調(diào)遞增時(shí)![]() 的最大值.
的最大值.
(1)∵![]() ,
,![]()
∴![]()
![]()
![]()
![]()
∴![]() ,即
,即![]()
![]()
∵![]()
∴![]()
∴當(dāng)![]() 時(shí),
時(shí),![]()
∴![]()
(2)解法1:∵![]()
∴![]() 為
為![]() 圖像的對稱軸
圖像的對稱軸
又![]()
∴
兩式相減得![]()
∴![]()
∵![]() 在
在![]() 單調(diào)遞增,令
單調(diào)遞增,令![]()
∴![]() 在
在![]() 單調(diào)遞增
單調(diào)遞增
∴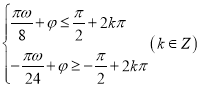 ,則
,則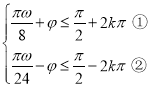 ,
,
①+②得![]()
∴![]()
∵![]()
∴當(dāng)![]() 時(shí)
時(shí)![]() 取到最大值為
取到最大值為![]()
解法2:![]() 在
在![]() 單調(diào)遞增
單調(diào)遞增
∴![]()
∴![]()
∵![]()
∴![]() 為
為![]() 圖像的對稱軸
圖像的對稱軸
又![]()
∴
兩式相加得![]()
∵![]()
∴![]() 或
或![]()
①當(dāng)![]() 時(shí),
時(shí),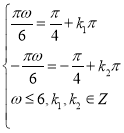 ,得
,得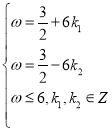 ,
,![]()
②當(dāng)![]() 時(shí)
時(shí)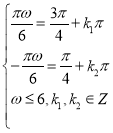 ,得
,得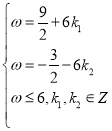 ,
,![]()
當(dāng)![]() ,
,![]() 時(shí)
時(shí)![]()
![]() 時(shí),
時(shí),![]()
則滿足條件![]() 在
在![]() 單調(diào)遞增,所以
單調(diào)遞增,所以![]() 的最大值為
的最大值為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某車間生產(chǎn)某種電子元件,如果生產(chǎn)出一件正品,可獲利200元,如果生產(chǎn)出一件次品,則損失100元.已知該車間制造電子元件的過程中,次品率![]() 與日產(chǎn)量
與日產(chǎn)量![]() 的函數(shù)關(guān)系是:
的函數(shù)關(guān)系是:![]() .
.
(1)寫出該車間的日盈利額![]() (元)與日產(chǎn)量
(元)與日產(chǎn)量![]() (件)之間的函數(shù)關(guān)系式;
(件)之間的函數(shù)關(guān)系式;
(2)為使日盈利額最大,該車間的日產(chǎn)量應(yīng)定為多少件?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在四棱錐![]() 中,
中,![]() 平面
平面![]() ,且底面
,且底面![]() 為邊長為2的菱形,
為邊長為2的菱形,![]() ,
,![]() .
.
(Ⅰ)記![]() 在平面
在平面![]() 內(nèi)的射影為
內(nèi)的射影為![]() (即
(即![]() 平面
平面![]() ),試用作圖的方法找出M點(diǎn)位置,并寫出
),試用作圖的方法找出M點(diǎn)位置,并寫出![]() 的長(要求寫出作圖過程,并保留作圖痕跡,不需證明過程和計(jì)算過程);
的長(要求寫出作圖過程,并保留作圖痕跡,不需證明過程和計(jì)算過程);

(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 為奇函數(shù),
為奇函數(shù),![]() 為常數(shù).
為常數(shù).
(1)求![]() 的值
的值
(2)判斷函數(shù)![]() 在
在![]() 上的單調(diào)性,并說明理由;
上的單調(diào)性,并說明理由;
(3)若對于區(qū)間![]() 上的每一個(gè)
上的每一個(gè)![]() 值,不等式
值,不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知矩形![]() 中,
中,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 上的點(diǎn),
上的點(diǎn),![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點(diǎn),現(xiàn)沿著
的中點(diǎn),現(xiàn)沿著![]() 翻折,使平面
翻折,使平面![]() 平面
平面![]() .
.
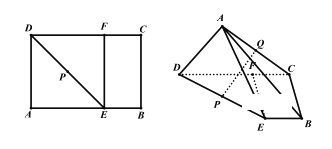
(1)![]() 為
為![]() 的中點(diǎn),求證:
的中點(diǎn),求證:![]() 平面
平面![]() .
.
(2)求點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的方程為
的方程為![]() ,過點(diǎn)
,過點(diǎn)![]() (
(![]() 為常數(shù))作拋物線
為常數(shù))作拋物線![]() 的兩條切線,切點(diǎn)分別為
的兩條切線,切點(diǎn)分別為![]() ,
,![]() .
.
(1)過焦點(diǎn)且在![]() 軸上截距為
軸上截距為![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點(diǎn),
兩點(diǎn),![]() ,
,![]() 兩點(diǎn)在
兩點(diǎn)在![]() 軸上的射影分別為
軸上的射影分別為![]() ,
,![]() ,且
,且![]() ,求拋物線
,求拋物線![]() 的方程;
的方程;
(2)設(shè)直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() .求證:
.求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于定義在![]() 上的函數(shù)
上的函數(shù)![]() ,如果對于任意的
,如果對于任意的![]() ,存在常數(shù)
,存在常數(shù)![]() 都有
都有![]() 成立,則稱
成立,則稱![]() 為函數(shù)
為函數(shù)![]() 在
在![]() 上的一個(gè)上界.已知函數(shù)
上的一個(gè)上界.已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),試判斷函數(shù)
時(shí),試判斷函數(shù)![]() 在
在![]() 上是否存在上界,若存在請求出該上界,若不存在請說明理由;
上是否存在上界,若存在請求出該上界,若不存在請說明理由;
(2)若函數(shù)![]() 在
在![]() 上的上界為3,求出實(shí)數(shù)
上的上界為3,求出實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國古代十進(jìn)制的算籌計(jì)數(shù)法,在世界數(shù)學(xué)史上是一個(gè)偉大的創(chuàng)造. 算籌實(shí)際上是一根根同樣長短的小木棍,用算籌表示數(shù)1~9的方法如圖:例如:163可表示為“![]() ”,27可表示為“
”,27可表示為“![]() ”.現(xiàn)有6根算籌,用來表示不能被10整除的兩位數(shù),算籌必須用完,則這樣的兩位數(shù)的個(gè)數(shù)為_________.
”.現(xiàn)有6根算籌,用來表示不能被10整除的兩位數(shù),算籌必須用完,則這樣的兩位數(shù)的個(gè)數(shù)為_________.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線斜率為
處的切線斜率為![]() ,求該切線方程;
,求該切線方程;
(2)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上恒成立,且存在
上恒成立,且存在![]() 使得
使得![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com