【題目】已知函數
（Ⅰ）若函數
的圖像在點
處的切線與直線
平行，求實數
的值；
（Ⅱ）討論函數
的單調性；
（Ⅲ）若在函數
定義域內，總有
成立，試求實數
的最大值.
【答案】(Ⅰ) 
；(Ⅱ)證明見解析；(Ⅲ) 
【解析】試題分析：（1）先根據導數幾何意義得
，解得實數
的值；（2）求導數并分解因式，根據a與1的大小分類討論導函數符號，根據導函數符號確定函數
的單調性；（3）先化簡不等式，并根據不等式恒成立轉化為對應函數最值問題： 
最大值不大于零，再利用導數求得函數最值
從而有
的最大值，最后利用導數求得
最大值，即得實數
的最大值.
試題解析：（Ⅰ）易得
，且
由題意，得
，解得
，
（Ⅱ）由（Ⅰ）得
，
①當
時， 
， 
函數
在
單調遞減，
②當
時，由
，得
；
由
，得
或
函數
在
上單調遞增，在
上單調遞減.
③當
時，同理，得
函數
在
上單調遞增，在
上單調遞減，
綜上，當
時，函數
在
單調遞減；
當
時，函數
在
上單調遞增，在
上單調遞減；
當
時，函數
在
上單調遞增，在
上單調遞減.
（Ⅲ）由題意，知
恒成立，
恒成立，
恒成立，
令
，則只需
，
由
，得
，
當
時， 
，此時，函數
在
上單調遞減；
當
時， 
，此時，函數
在
上單調遞減，
令
，則只需
由
，得
，此時， 
在
上單調遞減，
由
，得
，此時， 
在
上單調遞減，
，
即
故所求實數
的最大值為
黃岡小狀元解決問題天天練系列答案
三點一測快樂周計劃系列答案科目：高中數學 來源： 題型：
【題目】定義在
上的函數
，若
，有
，則稱函數
為定義在
上的非嚴格單增函數；若
，有
，則稱函數
為定義在
上的非嚴格單減函數. 
.
（1）若函數
為定義在
上的非嚴格單增函數，求實數
的取值范圍.
（2）若函數
為定義在
上的非嚴格單減函數，試解不等式
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某特色餐館開通了美團外賣服務，在一周內的某特色菜外賣份數
（份）與收入
（元）之間有如下的對應數據：
外賣份數 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
（1）畫出散點圖；
（2）求回歸直線方程；
（3）據此估計外賣份數為12份時，收入為多少元．
注：①參考公式：線性回歸方程系數公式
， 
；
②參考數據： 
， 
， 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】所謂正三棱錐，指的是底面為正三角形，頂點在底面上的射影為底面三角形中心的三棱錐，在正三棱錐S﹣ABC中，M是SC的中點，且AM⊥SB，底面邊長AB=2 
，則正三棱錐S﹣ABC的體積為 ， 其外接球的表面積為 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知命題P：x1 ， x2是方程x2﹣mx﹣1=0的兩個實根，且不等式a2+4a﹣3≤|x1﹣x2|對任意m∈R恒成立；命題q：不等式ax2+2x﹣1＞0有解，若命題p∨q為真，p∧q為假，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設圓
滿足：（1）截
軸所得弦長為2；（2）被
軸分成兩段圓弧，其弧長的比為
.在滿足條件（1）、（2）的所有圓中，圓心到直線
的距離最小的圓的方程為__________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某特色餐館開通了美團外賣服務，在一周內的某特色菜外賣份數
（份）與收入
（元）之間有如下的對應數據：
外賣份數 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
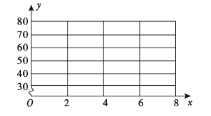
（1）畫出散點圖；
（2）求回歸直線方程；
（3）據此估計外賣份數為12份時，收入為多少元．
注：①參考公式：線性回歸方程系數公式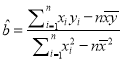
， 
；
②參考數據： 
， 
， 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】阿海準備購買“海馬”牌一輛小汽車，其中購車費用12.8萬元，每年的保險費、汽油費約為0.95萬元，年維修、保養費第一年是0.1萬元，以后逐年遞增0.1萬元．請你幫阿海計算一下這種汽車使用多少年，它的年平均費用最少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
