
【題目】某企業打算處理一批產品,這些產品每箱100件,以箱為單位銷售.已知這批產品中每箱出現的廢品率只有![]() 或者
或者![]() 兩種可能,兩種可能對應的概率均為0.5.假設該產品正品每件市場價格為100元,廢品不值錢.現處理價格為每箱8400元,遇到廢品不予更換.以一箱產品中正品的價格期望值作為決策依據.
兩種可能,兩種可能對應的概率均為0.5.假設該產品正品每件市場價格為100元,廢品不值錢.現處理價格為每箱8400元,遇到廢品不予更換.以一箱產品中正品的價格期望值作為決策依據.
(1)在不開箱檢驗的情況下,判斷是否可以購買;
(2)現允許開箱,有放回地隨機從一箱中抽取2件產品進行檢驗.
①若此箱出現的廢品率為![]() ,記抽到的廢品數為
,記抽到的廢品數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
②若已發現在抽取檢驗的2件產品中,其中恰有一件是廢品,判斷是否可以購買.
【答案】(1) 在不開箱檢驗的情況下,可以購買. (2) ①分布列見解析,0.4 ②不可以購買
【解析】
(1)求出在不開箱檢驗的情況下,一箱產品中正品的價格期望值,即得解;(2)①![]() 的可能取值為0,1,2,再求出對應的概率,即得
的可能取值為0,1,2,再求出對應的概率,即得![]() 的分布列和數學期望;②一箱產品中,設正品的價格的期望值為
的分布列和數學期望;②一箱產品中,設正品的價格的期望值為![]() ,求出
,求出![]() 即得解.
即得解.
(1)在不開箱檢驗的情況下,一箱產品中正品的價格期望值為:
![]() ,
,
∴在不開箱檢驗的情況下,可以購買.
(2)①![]() 的可能取值為0,1,2,
的可能取值為0,1,2,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 |
| 0.64 | 0.32 | 0.04 |
![]() .
.
②設事件![]() :發現在抽取檢驗的2件產品中,其中恰有一件是廢品,
:發現在抽取檢驗的2件產品中,其中恰有一件是廢品,
則![]() ,
,
一箱產品中,設正品的價格的期望值為![]() ,則
,則![]() ,
,
事件![]() :抽取的廢品率為
:抽取的廢品率為![]() 的一箱,
的一箱,
![]() ,
,
事件![]() :抽取的廢品率為
:抽取的廢品率為![]() 的一箱,
的一箱,
則![]() ,
,
∴![]() ,
,
∴已發現在抽取檢驗的2件產品中,其中恰有一件是廢品,不可以購買.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,離心率為
,離心率為![]() ,直線
,直線![]() 恒過
恒過![]() 的一個焦點
的一個焦點![]() .
.
(1)求![]() 的標準方程;
的標準方程;
(2)設![]() 為坐標原點,四邊形
為坐標原點,四邊形![]() 的頂點均在
的頂點均在![]() 上,
上,![]() 交于
交于![]() ,且
,且![]() ,若直線
,若直線![]() 的傾斜角的余弦值為
的傾斜角的余弦值為![]() ,求直線
,求直線![]() 與
與![]() 軸交點的坐標.
軸交點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中華人民共和國道路交通安全法》第![]() 條的相關規定:機動車行經人行道時,應當減速慢行;遇行人正在通過人行道,應當停車讓行,俗稱“禮讓斑馬線”《中華人民共和國道路交通安全法》第
條的相關規定:機動車行經人行道時,應當減速慢行;遇行人正在通過人行道,應當停車讓行,俗稱“禮讓斑馬線”《中華人民共和國道路交通安全法》第![]() 條規定:對不禮讓行人的駕駛員處以扣
條規定:對不禮讓行人的駕駛員處以扣![]() 分,罰款
分,罰款![]() 元的處罰.下表是某市一主干路口監控設備所抓拍的
元的處罰.下表是某市一主干路口監控設備所抓拍的![]() 個月內駕駛員不“禮讓斑馬線”行為統計數據:
個月內駕駛員不“禮讓斑馬線”行為統計數據:
月份 |
|
|
|
|
|
不“禮讓斑馬線”駕駛員人數 |
|
|
|
|
|
(1)請利用所給數據求不“禮讓斑馬線”駕駛員人數![]() 與月份
與月份![]() 之間的回歸直線方程
之間的回歸直線方程![]() ,并預測該路口
,并預測該路口![]() 月份的不“禮讓斑馬線”駕駛員人數;
月份的不“禮讓斑馬線”駕駛員人數;
(2)若從表中![]() 月份和
月份和![]() 月份的不“禮讓斑馬線”駕駛員中,采用分層抽樣方法抽取一個容量為
月份的不“禮讓斑馬線”駕駛員中,采用分層抽樣方法抽取一個容量為![]() 的樣本,再從這
的樣本,再從這![]() 人中任選
人中任選![]() 人進行交規調查,求抽到的兩人恰好來自同一月份的概率.
人進行交規調查,求抽到的兩人恰好來自同一月份的概率.
參考公式: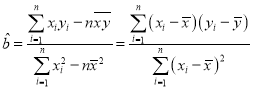 ,
,![]() .
.
參考數據:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】紅鈴蟲是棉花的主要害蟲之一,能對農作物造成嚴重傷害,每只紅鈴蟲的平均產卵數y和平均溫度x有關,現收集了以往某地的7組數據,得到下面的散點圖及一些統計量的值.(表中![]() )
)
平均溫度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 | ||
平均產卵數 | 7 | 11 | 21 | 24 | 66 | 115 | 325 | ||
|
|
|
|
| |||||
27.429 | 81.286 | 3.612 | 40.182 | 147.714 | |||||
(1)根據散點圖判斷,![]() 與
與![]() (其中
(其中![]() 自然對數的底數)哪一個更適宜作為平均產卵數y關于平均溫度x的回歸方程類型?(給出判斷即可,不必說明理由)并由判斷結果及表中數據,求出y關于x的回歸方程.(計算結果精確到小數點后第三位)
自然對數的底數)哪一個更適宜作為平均產卵數y關于平均溫度x的回歸方程類型?(給出判斷即可,不必說明理由)并由判斷結果及表中數據,求出y關于x的回歸方程.(計算結果精確到小數點后第三位)
(2)根據以往統計,該地每年平均溫度達到28℃以上時紅鈴蟲會造成嚴重傷害,需要人工防治,其他情況均不需要人工防治記該地每年平均溫度達到28℃以上的概率為![]() .
.
①記該地今后5年中,恰好需要3次人工防治的概率為![]() ,求
,求![]() 的最大值,并求出相應的概率p.
的最大值,并求出相應的概率p.
②當![]() 取最大值時,記該地今后5年中,需要人工防治的次數為X,求X的數學期望和方差.
取最大值時,記該地今后5年中,需要人工防治的次數為X,求X的數學期望和方差.
附:線性回歸方程系數公式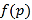 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠在2016年的“減員增效”中對部分人員實行分流,規定分流人員第一年可以到原單位領取工資的100%,從第二年起,以后每年只能在原單位按上一年的![]() 領取工資,該廠根據分流人員的技術特長,計劃創辦新的經濟實體,該經濟實體預計第一年屬投資階段,第二年每人可獲得
領取工資,該廠根據分流人員的技術特長,計劃創辦新的經濟實體,該經濟實體預計第一年屬投資階段,第二年每人可獲得![]() 元收入,從第三年起每人每年的收入可在上一年的基礎上遞增50%,如果某人分流后工資的收入每年
元收入,從第三年起每人每年的收入可在上一年的基礎上遞增50%,如果某人分流后工資的收入每年![]() 元,分流后進入新經濟實體,第
元,分流后進入新經濟實體,第![]() 年的收入為
年的收入為![]() 元;
元;
(1)求![]() 的通項公式;
的通項公式;
(2)當![]() 時,是否一定可以保證這個人分流一年后的收入永遠超過分流前的年收入?
時,是否一定可以保證這個人分流一年后的收入永遠超過分流前的年收入?
查看答案和解析>>
科目:高中數學 來源: 題型:
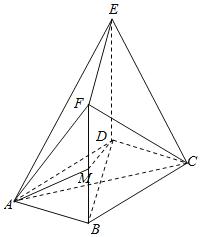
【題目】如圖,在多面體ABCDEF中,底面ABCD是邊長為2的菱形,∠BAD=60°,四邊形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M為線段BF上一點,且DM⊥平面ACE.
(1)求BM的長;
(2)求二面角A﹣DM﹣B的余弦值的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】廣東省2021年高考將實行“![]() ”模式,其最大特點就是取消文理科,除語文、數學、外語之外,從物理、歷史這2科中自由選擇一門科目;化學、生物、政治、地理這4科中自由選擇兩門科目作為選考科目.某研究機構為了了解學生對全理(選擇物理、化學、生物)的選擇是否與性別有關,從某學校高一年級的學生中隨機抽取男生、女生個25人進行模擬選科.經統計,選擇全理的人數比不選全理的人數多10人.
”模式,其最大特點就是取消文理科,除語文、數學、外語之外,從物理、歷史這2科中自由選擇一門科目;化學、生物、政治、地理這4科中自由選擇兩門科目作為選考科目.某研究機構為了了解學生對全理(選擇物理、化學、生物)的選擇是否與性別有關,從某學校高一年級的學生中隨機抽取男生、女生個25人進行模擬選科.經統計,選擇全理的人數比不選全理的人數多10人.
(1)請完成下面的![]() 列聯表:
列聯表:
選擇全理 | 不選擇全理 | 合計 | |
男生 | 5 | ||
女生 | |||
合計 |
(2)估計有多大把握認為選擇全理與性別有關,并說明理由;
(3)現從這50名學生中已經選取了男生3名,女生2名進行座談,從這5人中抽取2名代表作問卷調查,求至少抽到一名女生的概率.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:![]() ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com