
【題目】定義:由橢圓的兩個焦點和短軸的一個頂點組成的三角形稱為該橢圓的“特征三角形”;如果兩個橢圓的“特征三角形”是相似的,則稱這兩個橢圓是“相似橢圓”,并將三角形的相似比稱為橢圓的相似比,已知橢圓![]() .
.

(1)若橢圓![]() ,判斷
,判斷![]() 與
與![]() 相似?如果相似,求出
相似?如果相似,求出![]() 與
與![]() 的相似比;如果不相似,請說明理由;
的相似比;如果不相似,請說明理由;
(2)寫出與橢圓![]() 相似且焦點在
相似且焦點在![]() 軸上,短半軸長為
軸上,短半軸長為![]() 的橢圓
的橢圓![]() 的標準方程;若在橢圓
的標準方程;若在橢圓![]() 上存在兩點
上存在兩點![]() 、
、![]() 關(guān)于直線
關(guān)于直線![]() 對稱,求實數(shù)
對稱,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)如圖:直線![]() 與兩個“相似橢圓”
與兩個“相似橢圓”![]() 和
和![]() 分別交于點
分別交于點![]() 和點
和點![]() ,試在橢圓
,試在橢圓![]() 和橢圓
和橢圓![]() 上分別作出點
上分別作出點![]() 和點
和點![]() (非橢圓頂點),使
(非橢圓頂點),使![]() 和
和![]() 組成以
組成以![]() 為相似比的兩個相似三角形,寫出具體作法.(不必證明)
為相似比的兩個相似三角形,寫出具體作法.(不必證明)
【答案】(1)橢圓![]() 與
與![]() 相似,相似比為
相似,相似比為![]() ;(2)
;(2)![]() ;(3)見解析.
;(3)見解析.
【解析】
(1)由題意橢圓![]() 與
與![]() 相似,由橢圓
相似,由橢圓![]() 的特征三角形是腰長為4,底邊長為
的特征三角形是腰長為4,底邊長為![]() 的等腰三角形,能求出
的等腰三角形,能求出![]() 與
與![]() 的相似比.
的相似比.
(2)橢圓![]() 的方程為:
的方程為:![]() ,
,![]() ,設直線
,設直線![]() ,點
,點![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中點為
中點為![]() ,
,![]() ,由
,由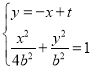 ,得
,得![]() ,由此利用韋達定理、根的判別式能求出實數(shù)
,由此利用韋達定理、根的判別式能求出實數(shù)![]() 的取值范圍.
的取值范圍.
(3)法1:過原點作直線![]() ,交橢圓
,交橢圓![]() 和橢圓
和橢圓![]() 于點
于點![]() 和點
和點![]() ,得到
,得到![]() 和
和![]() 即為所求相似三角形,且相似比為
即為所求相似三角形,且相似比為![]() .
.
法2:過點![]() 、點
、點![]() 分別做
分別做![]() 軸(或
軸(或![]() 軸)的垂線,交橢圓
軸)的垂線,交橢圓![]() 和橢圓
和橢圓![]() 點
點![]() 和點
和點![]() ,得到
,得到![]() 和
和![]() 即為所求相似三角形,且相似比為
即為所求相似三角形,且相似比為![]() .
.
解:(1)橢圓![]() 與
與![]() 相似.
相似.
因為![]() ,
,![]()
因為![]() ,
,![]()
因為橢圓![]() 的特征三角形是腰長為4,底邊長為
的特征三角形是腰長為4,底邊長為![]() 的等腰三角形,
的等腰三角形,
而橢圓![]() 的特征三角形是腰長為2,底邊長為
的特征三角形是腰長為2,底邊長為![]() 的等腰三角形,
的等腰三角形,
因此兩個等腰三角形相似,且相似比為![]() .
.
(2)橢圓![]() 的方程為:
的方程為:![]() ,
,![]() ,
,
設直線![]() ,點
,點![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中點為
中點為![]() ,
,![]() ,
,
則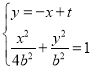 ,
,![]() ,
,
則![]() ,
,![]() ,
,
![]() 中點在直線
中點在直線![]() 上,
上,![]()
![]() ,
,![]() ,
,
即直線![]() 的方程為:
的方程為:![]() ,
,
由題意可知,直線![]() 與橢圓
與橢圓![]() 有兩個不同的交點,
有兩個不同的交點,
即方程![]() 有兩個不同的實數(shù)解,
有兩個不同的實數(shù)解,
![]()
![]() ,即
,即![]() .
.
(3)作法1:過原點作直線![]() ,交橢圓
,交橢圓![]() 和橢圓
和橢圓![]() 于點
于點![]() 和點
和點![]() ,
,
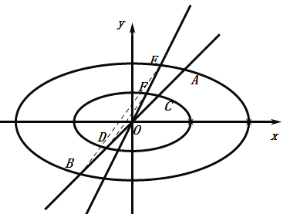
則![]() 和
和![]() 即為所求相似三角形,且相似比為
即為所求相似三角形,且相似比為![]() .
.
作法2:過點![]() 、點
、點![]() 分別做
分別做![]() 軸(或
軸(或![]() 軸)的垂線,交橢圓
軸)的垂線,交橢圓![]() 和橢圓
和橢圓![]() 點
點![]() 和點
和點![]() ,
,

則![]() 和
和![]() 即為所求相似三角形,且相似比為
即為所求相似三角形,且相似比為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,![]() 是某海灣旅游區(qū)的一角,其中
是某海灣旅游區(qū)的一角,其中![]() ,為了營造更加優(yōu)美的旅游環(huán)境,旅游區(qū)管委會決定在直線海岸
,為了營造更加優(yōu)美的旅游環(huán)境,旅游區(qū)管委會決定在直線海岸![]() 和
和![]() 上分別修建觀光長廊
上分別修建觀光長廊![]() 和AC,其中
和AC,其中![]() 是寬長廊,造價是
是寬長廊,造價是![]() 元/米,
元/米,![]() 是窄長廊,造價是
是窄長廊,造價是![]() 元/米,兩段長廊的總造價為120萬元,同時在線段
元/米,兩段長廊的總造價為120萬元,同時在線段![]() 上靠近點
上靠近點![]() 的三等分點
的三等分點![]() 處建一個觀光平臺,并建水上直線通道
處建一個觀光平臺,并建水上直線通道![]() (平臺大小忽略不計),水上通道的造價是
(平臺大小忽略不計),水上通道的造價是![]() 元/米.
元/米.
(1) 若規(guī)劃在三角形![]() 區(qū)域內(nèi)開發(fā)水上游樂項目,要求
區(qū)域內(nèi)開發(fā)水上游樂項目,要求![]() 的面積最大,那么
的面積最大,那么![]() 和
和![]() 的長度分別為多少米?
的長度分別為多少米?
(2) 在(1)的條件下,建直線通道![]() 還需要多少錢?
還需要多少錢?

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2019年4月25日-27日,北京召開第二屆“一帶一路”國際高峰論壇,組委會要從6個國內(nèi)媒體團和3個國外媒體團中選出3個媒體團進行提問,要求這三個媒體團中既有國內(nèi)媒體團又有國外媒體團,且國內(nèi)媒體團不能連續(xù)提問,則不同的提問方式的種數(shù)為 ( )
A. 198B. 268C. 306D. 378
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某公司為了預測下月產(chǎn)品銷售情況,找出了近7個月的產(chǎn)品銷售量![]() (單位:萬件)的統(tǒng)計表:
(單位:萬件)的統(tǒng)計表:
月份代碼 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
銷售量 |
|
|
|
|
|
|
|
但其中數(shù)據(jù)污損不清,經(jīng)查證![]() ,
,![]() ,
, .
.
(1)請用相關(guān)系數(shù)說明銷售量![]() 與月份代碼
與月份代碼![]() 有很強的線性相關(guān)關(guān)系;
有很強的線性相關(guān)關(guān)系;
(2)求![]() 關(guān)于
關(guān)于![]() 的回歸方程(系數(shù)精確到0.01);
的回歸方程(系數(shù)精確到0.01);
(3)公司經(jīng)營期間的廣告宣傳費![]() (單位:萬元)(
(單位:萬元)(![]() ),每件產(chǎn)品的銷售價為10元,預測第8個月的毛利潤能否突破15萬元,請說明理由.(毛利潤等于銷售金額減去廣告宣傳費)
),每件產(chǎn)品的銷售價為10元,預測第8個月的毛利潤能否突破15萬元,請說明理由.(毛利潤等于銷售金額減去廣告宣傳費)
參考公式及數(shù)據(jù):![]() ,相關(guān)系數(shù)
,相關(guān)系數(shù) ,當
,當![]() 時認為兩個變量有很強的線性相關(guān)關(guān)系,回歸方程
時認為兩個變量有很強的線性相關(guān)關(guān)系,回歸方程![]() 中斜率和截距的最小二乘估計公式分別為
中斜率和截距的最小二乘估計公式分別為 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 滿足:
滿足:![]()
(1)求:![]() ,
,
(2)猜想數(shù)列![]() 的通項公式,并用數(shù)學歸納法證明;
的通項公式,并用數(shù)學歸納法證明;
(3)若![]() 且
且![]() 對于
對于![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】南北朝時代的偉大科學家祖暅在數(shù)學上有突出貢獻,他在實踐的基礎(chǔ)上提出祖暅原理:“冪勢既同,則積不容異”. 其含義是:夾在兩個平行平面之間的兩個幾何體,被平行于這兩個平行平面的任意平面所截,如果截得的兩個截面的面積總相等,那么這兩個幾何體的體積相等.如圖,夾在兩個平行平面之間的兩個幾何體的體積分別為![]() ,被平行于這兩個平面的任意平面截得的兩個截面面積分別為
,被平行于這兩個平面的任意平面截得的兩個截面面積分別為![]() ,則“
,則“![]() 相等”是“
相等”是“![]() 總相等”的
總相等”的

A. 充分而不必要條件B. 必要而不充分條件
C. 充分必要條件D. 既不充分也不必要條件
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知圓C:![]() 內(nèi)有一點P(2,2),過點P作直線l交圓C于A、B兩點.
內(nèi)有一點P(2,2),過點P作直線l交圓C于A、B兩點.
(1)當l經(jīng)過圓心C時,求直線l的方程;
(2)當直線l的傾斜角為45時,求弦AB的長.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com