【題目】設函數f（x）=Asin（2x+ 
）（x∈R）的圖象過點P（ 
，﹣2）． （Ⅰ）求f（x）的解析式；
（Ⅱ）已知f（ 
+ 
）= 
，﹣ 
＜a＜0，求cos（a﹣ 
）的值．
【答案】解：（Ⅰ）∵f（x）的圖象過點P（ 
，﹣2）， ∴f（ ）=Asin（2× + 
）=Asin 
=﹣2
∴A=2
故f（x）的解析式為f（x）=2sin（2x+ ）
（Ⅱ）∵f（ 
+ 
）=2cosα= 
，∴cosα= 
，
∵﹣ 
＜a＜0，∴sinα=﹣ 
（9分）
∴cos（a﹣ 
）=cosαcos +sinαsin =﹣ 
【解析】（Ⅰ）根據f（x）的圖象過點P（ 
，﹣2），可得f（ ）=Asin（2× + 
）=Asin 
=﹣2，從而可求f（x）的解析式為；（Ⅱ）根據f（ 
+ 
）=2cosα= 
，可得cosα= 
，結合﹣ 
＜a＜0，可得sinα=﹣ 
，再利用差角的余弦公式，即可求得結論．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知三棱柱ABC﹣A1B1C1的直觀圖和三視圖如圖所示，E是棱CC1上一點． 
（1）若CE=2EC1 ， 求三棱錐E﹣ACB1的體積．
（2）若E是CC1的中點，求C到平面AEB1的距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x）的定義域為開區間（a，b），導函數f′（x）在（a，b）內的圖象如圖所示，則函數f（x）在開區間（a，b）內有極大值點（ ） 
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在側棱和底面垂直的三棱柱ABC﹣A1B1C1中，AB=1，AC= 
，BC=2，AA1= 
，點P為CC1的中點．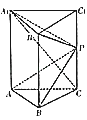 
（1）求證：A1C⊥平面ABP；
（2）求平面ABP與平面A1B1P所成二面角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】盒子中有大小相同的球6個，其中標號為1的球2個，標號為2的球3個．標號為3的球1個，第一次從盒子中任取1個球，放回后第二次再任取1個球 （假設取到每個球的可能性都相同）．記第一次與第二次取到球的標號之和為ξ．
（1）求隨機變量ξ的分布列：
（2）求隨機變量ξ的期望Eξ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為增強市民的節能環保意識，某市面向全市征召義務宣傳志愿者．從符合條件的500名志愿者中隨機抽取100名志愿者，其年齡頻率分布直方圖如圖所示，其中年齡分組區間是：[20，25），[25，30），[30，35），[35，40），[40，45]．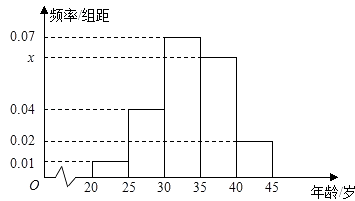
（Ⅰ）求圖中x的值并根據頻率分布直方圖估計這500名志愿者中年齡在[35，40）歲的人數；
（Ⅱ）在抽出的100名志愿者中按年齡采用分層抽樣的方法抽取20名參加中心廣場的宣傳活動，再從這20名中采用簡單隨機抽樣方法選取3名志愿者擔任主要負責人．記這3名志愿者中“年齡低于35歲”的人數為X，求X的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在某大學自主招生考試中，所有選報Ⅱ類志向的考生全部參加了“數學與邏輯”和“閱讀與表達”兩個科目的考試，成績分為
， 
， 
， 
， 
五個等級．某考場考生兩科的考試成績的數據如下圖所示，其中“數學與邏輯”科目的成績為
的考生有
人．
（Ⅰ）求該考場考生中“閱讀與表達”科目中成績為
的人數．
（Ⅱ）若等級
， 
， 
， 
， 
分別對應
分， 
分， 
分， 
分， 
分．
（ⅰ）求該考場考生“數學與邏輯”科目的平均分．
（ⅱ）若該考場共有
人得分大于
分，其中有
人
分， 
人
分， 
人
分．
從這
人中隨機抽取兩人，求兩人成績之和的分布列和數學期望．
科目：數學與邏輯 | 科目：閱讀與表達 |
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=2acos2x+2 
bsinxcosx，且f（0）=2，f（ 
）= +1．
（1）求f（x）的最大值及單調遞減區間；
（2）若α≠β，α，β∈（0，π），且f（α）=f（β），求tan（α+β）的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
