【題目】在△ABC中，a，b，c分別是角A，B，C的對邊，A，B是銳角，c=10，且 
．
（1）證明角C=90°；
（2）求△ABC的面積．
【答案】
（1）證明：在△ABC中，∵ 
．
∴根據正弦定理得 
，整理為sinAcosA=sinBcosB，即sin2A=sin2B．
∵0＜2A，2B＜π，
∴2A=2B，或2A+2B=π．
∵ 
，A≠B，
∴A+B= 
，即∠C=90°
（2）解：∵△ABC是以角C為直角的直角三角形，且c=10， ，a2+b2=c2，
∴可得：（ 
a）2+a2=100，
∴求得a=6，b=8．
∴△ABC的面積S= 
ab=24．
【解析】（1）根據正弦定理，二倍角公式化簡已知可得sin2A=sin2B，結合角的范圍可得2A=2B，或2A+2B=π，由 ，可得A≠B，從而可求A+B= ，即可得解．（2）由（1）及已知，利用勾股定理可求a，b的值，進而利用三角形面積公式即可計算得解．
【考點精析】解答此題的關鍵在于理解正弦定理的定義的相關知識，掌握正弦定理:
．
科目：高中數學 來源： 題型：
【題目】如圖所示，在四棱錐P﹣ABCD中，底面ABCD為矩形，PA⊥平面ABCD，點E在線段PC上，PC⊥平面BDE．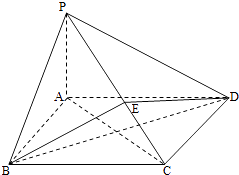 
（1）證明：BD⊥平面PAC；
（2）若PA=1，AD=2，求二面角B﹣PC﹣A的正切值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x2+2ax+2，x∈[﹣5，5]．
（1）當a=﹣1時，求函數f（x）的單調遞增區間；
（2）求實數a的取值范圍，使y=f（x）在區間[﹣5，5]上是單調函數．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【2017廣東佛山二模】已知橢圓
：
（
）的焦距為4，左、右焦點分別為
、
，且
與拋物線
：
的交點所在的直線經過
.
（Ⅰ）求橢圓
的方程；
（Ⅱ）分別過
、
作平行直線
、
，若直線
與
交于
，
兩點，與拋物線
無公共點，直線
與
交于
，
兩點，其中點
，
在
軸上方，求四邊形
的面積的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】公差不為零的等差數列{an}中，a3=7，又a2 ， a4 ， a9成等比數列．
（1）求數列{an}的通項公式．
（2）設bn=2 
，求數列{bn}的前n項和Sn ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
