
【題目】已知函數f(x)=lnx﹣a(x﹣1),a∈R
(1)討論函數f(x)的單調性;
(2)當x≥1時,f(x)≤ ![]() 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.
【答案】
(1)
解: f(x)的定義域為(0,+∞), ![]() ,
,
若a≤0,則f′(x)>0,∴f(x)在(0,+∞)上單調遞增,
若a>0,則由f′(x)=0,得x= ![]() ,
,
當x∈(0, ![]() )時,f′(x)>0,
)時,f′(x)>0,
當x∈( ![]() )時,f′(x)<0,
)時,f′(x)<0,
∴f(x)在(0, ![]() )上單調遞增,在(
)上單調遞增,在( ![]() ,+∞)單調遞減.
,+∞)單調遞減.
所以當a≤0時,f(x)在(0,+∞)上單調遞增,
當a>0時,f(x)在(0, ![]() )上單調遞增,在(
)上單調遞增,在( ![]() ,+∞)單調遞減.
,+∞)單調遞減.
(2)
解:f(x)﹣ ![]() =
= ![]() ,
,
令g(x)=xlnx﹣a(x2﹣1),(x≥1),
g′(x)=lnx+1﹣2ax,令F(x)=g′(x)=lnx+1﹣2ax,
![]() ,
,
①若a≤0,F′(x)>0,g′(x)在[1,+∞)遞增,
g′(x)≥g′(1)=1﹣2a>0,
∴g(x)在[1,+∞)遞增,g(x)≥g(1)=0,
從而f(x)﹣ ![]() 不符合題意.
不符合題意.
②若0<a< ![]() ,當x∈(1,
,當x∈(1, ![]() ),F′(x)>0,
),F′(x)>0,
∴g′(x)在(1, ![]() )遞增,
)遞增,
從而g′(x)>g′(1)=1﹣2a,
∴g(x)在[1,+∞)遞增,g(x)≥g(1)=0,
從而f(x)﹣ ![]() 不符合題意.
不符合題意.
③若a ![]() ,F′(x)≤0在[1,+∞)恒成立,
,F′(x)≤0在[1,+∞)恒成立,
∴g′(x)在[1,+∞)遞減,g′(x)≤g′(1)=1﹣2a≤0,
從而g9x)在[1,+∞)遞減,
∴g(x)≤g(1)=0,f(x)﹣ ![]() ≤0,
≤0,
綜上所述,a的取值范圍是[ ![]() ).
).
【解析】(1)f(x)的定義域為(0,+∞), ![]() ,若a≤0,f(x)在(0,+∞)上單調遞增;若a>0時,f(x)在(0,
,若a≤0,f(x)在(0,+∞)上單調遞增;若a>0時,f(x)在(0, ![]() )上單調遞增,在(
)上單調遞增,在( ![]() ,+∞)單調遞減.(2)f(x)﹣
,+∞)單調遞減.(2)f(x)﹣ ![]() =
= ![]() ,令g(x)=xlnx﹣a(x2﹣1),(x≥1),g′(x)=lnx+1﹣2ax,令F(x)=g′(x)=lnx+1﹣2ax,
,令g(x)=xlnx﹣a(x2﹣1),(x≥1),g′(x)=lnx+1﹣2ax,令F(x)=g′(x)=lnx+1﹣2ax, ![]() ,由此進行分類討論,能求出實數a的取值范圍.
,由此進行分類討論,能求出實數a的取值范圍.
【考點精析】解答此題的關鍵在于理解利用導數研究函數的單調性的相關知識,掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減.
在這個區間單調遞減.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:
【題目】已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.現給出如下結論:
①f(0)f(1)>0; ②f(0)f(1)<0;
③f(0)f(3)>0; ④f(0)f(3)<0.
其中正確結論的序號是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的個數有( )
①用 刻畫回歸效果,當
刻畫回歸效果,當![]() 越大時,模型的擬合效果越差;反之,則越好;
越大時,模型的擬合效果越差;反之,則越好;
②可導函數![]() 在
在![]() 處取得極值,則
處取得極值,則![]() ;
;
③歸納推理是由特殊到一般的推理,而演繹推理是由一般到特殊的推理;
④綜合法證明數學問題是“由因索果”,分析法證明數學問題是“執果索因”.
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年1曰8日,中共中央、國務院隆重舉行國家科學技術獎勵大會,在科技界引發熱烈反響,自主創新正成為引領經濟社會發展的強勁動力.某科研單位在研發新產品的過程中發現了一種新材料,由大數據測得該產品的性能指標值![]() 與這種新材料的含量
與這種新材料的含量![]() (單位:克)的關系為:當
(單位:克)的關系為:當![]() 時,
時, ![]() 是
是![]() 的二次函數;當
的二次函數;當![]() 時,
時, ![]() .測得數據如表(部分)
.測得數據如表(部分)
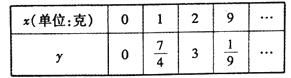
(1)求![]() 關于
關于![]() 的函數關系式
的函數關系式![]() ;
;
(2)其函數![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,以O為極點,x軸正半軸為極軸建立極坐標系.曲線C的參數方程為 ![]() (為參數,且0≤<2π),曲線l的極坐標方程為ρ=
(為參數,且0≤<2π),曲線l的極坐標方程為ρ= ![]() (k是常數,且k∈R).
(k是常數,且k∈R).
(1)求曲線C的普通方程和曲線l直角坐標方程;
(2)若曲線l被曲線C截的弦是以( ![]() ,1)為中點,求k的值.
,1)為中點,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 及函數
及函數![]() (a,b,c∈R),若a>b>c且a+b+c=0.
(a,b,c∈R),若a>b>c且a+b+c=0.
(1)證明:f(x)的圖像與g(x)的圖像一定有兩個交點;
(2)請用反證法證明:![]() ;
;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設關于某設備的使用年限![]() (年)和所支出的維修費用
(年)和所支出的維修費用![]() (萬元)有如下統計資料:
(萬元)有如下統計資料:
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由資料知, ![]() 對
對![]() 呈線性相關關系,試求:
呈線性相關關系,試求:
(1)回歸直線方程;
(2)估計使用年限為10年時,維修費用約是多少?
參考公式:回歸直線方程: ![]() .其中
.其中
(注: ![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com