
【題目】設常數![]() ,函數
,函數![]() .
.
(1)令![]() 時,求
時,求![]() 的最小值,并比較
的最小值,并比較![]() 的最小值與零的大小;
的最小值與零的大小;
(2)求證:![]() 在
在![]() 上是增函數;
上是增函數;
(3)求證:當![]() 時,恒有
時,恒有![]() .
.
【答案】(1)最小值為![]() ,最小值大于零.(2)證明見解析.(3)證明見解析
,最小值大于零.(2)證明見解析.(3)證明見解析
【解析】
(1)對函數![]() 進行求導,確定函數
進行求導,確定函數![]() 的解析式,再對函數
的解析式,再對函數![]() 求導,列表判斷出該函數的單調性以及極值,最后確定函數
求導,列表判斷出該函數的單調性以及極值,最后確定函數![]() 的最小值,再判斷
的最小值,再判斷![]() 的最小值與零的大小即可;
的最小值與零的大小即可;
(2)利用(1)中的結論,可以判斷出函數![]() 的正負性,進而能證明出
的正負性,進而能證明出![]() 的單調性;
的單調性;
(3)利用(2)中的結論進行證明即可.
(1)因為![]() ,
,
所以![]() .
.
所以![]() ,
,
所以![]() ,令
,令![]() ,得
,得![]() .
.
列表如下:
|
| 2 |
|
|
| 0 |
|
| 減 | 極小值 | 增 |
所以![]() 在
在![]() 處取得極小值
處取得極小值![]() ,
,
即![]() 的最小值為
的最小值為![]() ,
,
因為![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 即
即![]() 的最小值大于零.
的最小值大于零.
(2)由(1)知,![]() 的最小值為正數,
的最小值為正數,
所以對一切![]() ,恒有
,恒有![]() .
.
從而當![]() 時,恒有
時,恒有![]() ,故
,故![]() 在
在![]() 上是增函數.
上是增函數.
(3)由(2)知![]() 在
在![]() 上是增函數,
上是增函數,
所以當![]() 時,
時,![]() .
.
又![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
故當![]() 時,恒有
時,恒有![]() .
.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】雅山中學采取分層抽樣的方法從應屆高三學生中按照性別抽出20名學生作為樣本,其選報文科理科的情況如下表所示.
男 | 女 | |
文科 | 2 | 5 |
理科 | 10 | 3 |
(Ⅰ)若在該樣本中從報考文科的學生中隨機地選出3人召開座談會,試求3人中既有男生也有女生的概率;
(Ⅱ)用假設檢驗的方法分析有多大的把握認為雅山中學的高三學生選報文理科與性別有關?
參考公式和數據:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為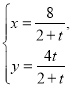 (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若射線![]() (
(![]() )與直線
)與直線![]() 和曲線
和曲線![]() 分別交于
分別交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖是一個![]() 的方格(其中心的方格線已被劃去).一只青蛙停在
的方格(其中心的方格線已被劃去).一只青蛙停在![]() 格處,從某一時刻起,青蛙每隔一秒鐘就跳到與它所在方格有公共邊的另一方格內,直至跳到
格處,從某一時刻起,青蛙每隔一秒鐘就跳到與它所在方格有公共邊的另一方格內,直至跳到![]() 格才停下..若青蛙經過每一個方格不超過一次,則青蛙的跳法總數為________.
格才停下..若青蛙經過每一個方格不超過一次,則青蛙的跳法總數為________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高考改革后,學生除了語數外三門必選外,可在A類科目:物理、化學、生物和B類科目:政治、地理、歷史共6個科目中任選3門.
(1)若小明同學已經確定選了物理,現在他還要從剩余的5科中再選2科,則他在歷史與地理兩科中至少選一科的概率?
(2)求小明同學選A類科目數X的分布列、數學期望和方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖![]() ,在邊長為
,在邊長為![]() 的菱形
的菱形![]() 中,
中,![]() ,現沿對角線
,現沿對角線![]() 把
把![]() 翻折到
翻折到![]() 的位置得到四面體
的位置得到四面體![]() ,如圖
,如圖![]() 所示.已知
所示.已知![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 是線段
是線段![]() 上的點,且
上的點,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com