
【題目】已知函數![]() .
.
(1)當![]() 時,求
時,求![]() 的圖象在
的圖象在![]() 處的切線方程;
處的切線方程;
(2)若函數![]() 在
在![]() 上有兩個零點,求實數m的取值范圍;
上有兩個零點,求實數m的取值范圍;
(3)若對區間![]() 內任意兩個不等的實數
內任意兩個不等的實數![]() ,
,![]() ,不等式
,不等式![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)求出函數的導數,利用導數的幾何意義即可求出函數![]() 在
在![]() 處的切線方程
處的切線方程
(2)先通過求導,研究函數![]() 的單調性,然后利用函數
的單調性,然后利用函數![]() 在
在![]() 上有兩個零點可得直線
上有兩個零點可得直線![]() 與
與![]() 的圖像有兩個交點,從而得到
的圖像有兩個交點,從而得到 ,求解即可
,求解即可
(3)不妨設![]() ,
,![]() 恒成立等價于
恒成立等價于![]() ,化簡為
,化簡為![]() ,然后,令
,然后,令![]() ,然后判斷
,然后判斷![]() 的單調性即可求解
的單調性即可求解
(1)當![]() 時,
時,![]() ,
,![]() ,切點坐標為
,切點坐標為![]() ,
,
切線的斜率![]() ,則切線方程為
,則切線方程為![]() ,即
,即![]() .
.
(2)![]() ,則
,則![]() ,
,
![]() ,故
,故![]() 時,
時,![]() .
.
當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() .
.
故![]() 在
在![]() 處取得極大值
處取得極大值![]() .
.
又![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,
![]() 在
在![]() 上的最小值是
上的最小值是![]() .
.
![]()
![]() 在
在![]() 上有兩個零點的條件是
上有兩個零點的條件是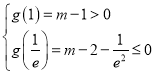
解得![]()
實數m的取值范圍是![]()
(3)不妨設![]() ,
,![]() 恒成立等價于
恒成立等價于![]() ,即
,即![]() .
.
令![]() ,由
,由![]() ,
,![]() 具有任意性知,
具有任意性知,![]() 在區間
在區間![]() 內單調遞減,
內單調遞減,
![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
![]() ,
,![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,則
,則![]()
![]() 在
在![]() 上單調遞增,則
上單調遞增,則![]() ,
,
實數a的取值范圍是![]()


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程:
的參數方程: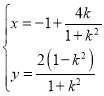 (
(![]() 為參數),以坐標原點為極點,以
為參數),以坐標原點為極點,以![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程;
的普通方程;
(2)過曲線![]() 上一點
上一點![]() 作直線
作直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,中點為
兩點,中點為![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+4[sin(θ+![]() )]x﹣2,θ∈[0,2π].
)]x﹣2,θ∈[0,2π].
(Ⅰ)若函數f(x)為偶函數,求tanθ的值;
(Ⅱ)若f(x)在[﹣![]() ,1]上是單調函數,求θ的取值范圍.
,1]上是單調函數,求θ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形![]() 為平行四邊形,
為平行四邊形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 是
是![]() 的中點.
的中點.
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 與
與![]() 所成的角為
所成的角為![]() ? 若存在,求出
? 若存在,求出![]() 的長度;若不存在,請說明理由.
的長度;若不存在,請說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 過點
過點![]() ,拋物線
,拋物線![]() 在
在![]() 處的切線交
處的切線交![]() 軸于點
軸于點![]() ,過點
,過點![]() 作直線
作直線![]() 與拋物線
與拋物線![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() ,直線
,直線![]() 、
、![]() 、
、![]() 分別與拋物線的準線交于點
分別與拋物線的準線交于點![]() 、
、![]() 、
、![]() ,其中
,其中![]() 為坐標原點.
為坐標原點.
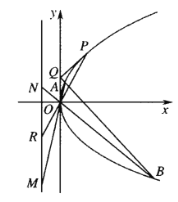
(Ⅰ)求拋物線![]() 的方程及其準線方程,并求出點
的方程及其準線方程,并求出點![]() 的坐標;
的坐標;
(Ⅱ)求證:![]() 為線段
為線段![]() 的中點.
的中點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 與過其右焦點F(1,0)的直線交于不同的兩點A,B,線段AB的中點為D,且直線l與直線OD的斜率之積為
與過其右焦點F(1,0)的直線交于不同的兩點A,B,線段AB的中點為D,且直線l與直線OD的斜率之積為![]() .
.
(1)求C的方程;
(2)設橢圓的左頂點為M,kMA,kMB分別表示直線MA,MB的斜率,求證![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年9月25日.阿里巴巴在杭州云棲大會上正式對外發布了含光800AI芯片,在業界標準的ResNet -50測試中,含光800推理性能達到78563lPS,比目前業界最好的AI芯片性能高4倍;能效比500 IPS/W,是第二名的3.3倍.在國內集成電路產業發展中,集成電路設計產業始終是國內集成電路產業中最具發展活力的領域,增長也最為迅速.如圖是2014-2018年中國集成電路設計產業的銷售額(億元)及其增速(%)的統計圖,則下面結論中正確的是( )
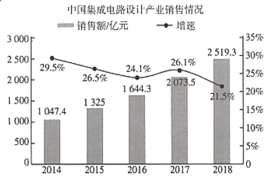
A.2014-2018年,中國集成電路設計產業的銷售額逐年增加
B.2014-2017年,中國集成電路設計產業的銷售額增速逐年下降
C.2018年中國集成電路設計產業的銷售額的增長率比2015年的高
D.2018年與2014年相比,中國集成電路設計產業銷售額的增長率約為110%
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,將曲線方程![]() ,先向左平移2個單位,再向上平移2個單位,得到曲線C.
,先向左平移2個單位,再向上平移2個單位,得到曲線C.
(1)點M(x,y)為曲線C上任意一點,寫出曲線C的參數方程,并求出![]() 的最大值;
的最大值;
(2)設直線l的參數方程為![]() ,(t為參數),又直線l與曲線C的交點為E,F,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段EF的中點且與l垂直的直線的極坐標方程.
,(t為參數),又直線l與曲線C的交點為E,F,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段EF的中點且與l垂直的直線的極坐標方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com