Question

已知E，F分別為正方體ABCD-A₁B₁C₁D的棱AB，AA₁上的點，且AE=

1

2

AB，AF=

1

3

AA₁，M，N分別為線段D₁E和線段C₁F上的點，則與平面ABCD平行的直線MN有（　　）

• A、1條
• B、3條
• C、6條
• D、無數條

Answer 1

考點：直線與平面平行的性質

專題：空間位置關系與距離

分析：取BH=

1

3

BB₁，連接FH，在D₁E上任取一點M，過M在面D₁HE中，作MG平行于HO，其中O滿足線段OE=

1

3

D₁E，再過G作GN∥FH，交C₁F于N，連接MN，根據線面平行的判定定理，得到GM∥平面ABCD，NG∥平面ABCD，再根據面面平行的判斷定理得到平面MNG∥平面ABCD，由面面平行的性質得到則MN∥平面ABCD，由于M是任意的，故MN有無數條．

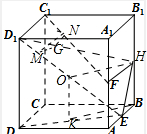
解答： 解：取BH=

1

3

BB₁，連接FH，則FH∥C₁D
連接HE，在D₁E上任取一點M，
過M在面D₁HE中，作MG∥HO，交D₁H于G，
其中O為線段OE=

1

3

D₁E
再過G作GN∥FH，交C₁F于N，連接MN，
由于GM∥HO，HO∥KB，KB?平面ABCD，
GM?平面ABCD，
所以GM∥平面ABCD，
同理由NG∥FH，可推得NG∥平面ABCD，
由面面平行的判定定理得，平面MNG∥平面ABCD，
則MN∥平面ABCD．
由于M為D₁E上任一點，故這樣的直線MN有無數條．
故選D．

點評：本題考查空間直線與平面的位置關系，主要是直線與平面平行的判斷和面面平行的判定與性質，考查空間想象能力和簡單推理能力．