【題目】已知集合
.
（1）若
，求
的概率；
（2）若
，求
的概率.
科目：高中數學 來源： 題型：
【題目】設f（x）與g（x）是定義在同一區間[a，b]上的兩個函數，若函數y=f（x）﹣g（x）在x∈[a，b]上有兩個不同的零點，則稱f（x）和g（x）在[a，b]上是“關聯函數”，區間[a，b]稱為“關聯區間”．若f（x）=x2﹣3x+4與g（x）=2x+m在[0，3]上是“關聯函數”，則m的取值范圍 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=lnx﹣mx+m，m∈R．
（1）已知函數f（x）在點（l，f（1））處與x軸相切，求實數m的值；
（2）求函數f（x）的單調區間；
（3）在（1）的結論下，對于任意的0＜a＜b，證明： 
＜ 
﹣1．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P﹣ABCD中，底面ABCD為直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q為AD的中點，M是棱PC上的點，PA=PD=2，BC= 
AD=1，CD= 
． 
（1）求證：平面PQB⊥平面PAD；
（2）若M為棱PC的中點，求異面直線AP與BM所成角的余弦值；
（3）若二面角M﹣BQ﹣C大小為30°，求QM的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖,四棱柱ABCD－A1B1C1D1的底面ABCD是正方形, O為底面中心, A1O⊥平面ABCD,
.
（1）證明: A1BD // 平面CD1B1;
（2）求三棱柱ABD－A1B1D1的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知a＞0且滿足不等式22a+1＞25a﹣2．
（1）求實數a的取值范圍；
（2）求不等式loga（3x+1）＜loga（7﹣5x）；
（3）若函數y=loga（2x﹣1）在區間[1，3]有最小值為﹣2，求實數a的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學利用周末組織教職員工進行了一次秋季登山健身的活動，有N人參加，現將所有參加者按年齡情況分為[20，25），[25，30），[30，35），[35，40），[40，45），[45，50），[50，55）等七組，其頻率分布直方圖如下所示．已知[35，40）這組的參加者是8人．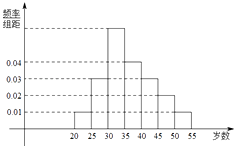 
（1）求N和[30，35）這組的參加者人數N1；
（2）已知[30，35）和[35，40）這兩組各有2名數學教師，現從這兩個組中各選取2人擔任接待工作，設兩組的選擇互不影響，求兩組選出的人中都至少有1名數學老師的概率；
（3）組織者從[45，55）這組的參加者（其中共有4名女教師，其余全為男教師）中隨機選取3名擔任后勤保障工作，其中女教師的人數為x，求x的分布列和均值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
