
【題目】設函數f(x)=|2x+1|+|x﹣a|,a∈R. (Ⅰ)當a=2時,求不等式f(x)<4的解集.
(Ⅱ)當a< ![]() 時,對于x∈(﹣∞,﹣
時,對于x∈(﹣∞,﹣ ![]() ],都有f(x)+x≥3成立,求a的取值范圍.
],都有f(x)+x≥3成立,求a的取值范圍.
【答案】解:(1)令|2x+1|=0,解得x=﹣ ![]() ,令|x﹣2|=0,解得x=2. 當x≥2時,原不等式化為:2x+1+x﹣2<4,解得x
,令|x﹣2|=0,解得x=2. 當x≥2時,原不等式化為:2x+1+x﹣2<4,解得x ![]() ,此時無解;
,此時無解;
當 ![]() <x<2時,原不等式化為:2x+1+2﹣x<4,解得x<1,可得
<x<2時,原不等式化為:2x+1+2﹣x<4,解得x<1,可得 ![]() <x<1;
<x<1;
當 ![]() 時,原不等式化為:﹣2x﹣1+2﹣x<4,解得x>﹣1,可得﹣1<x≤
時,原不等式化為:﹣2x﹣1+2﹣x<4,解得x>﹣1,可得﹣1<x≤ ![]() .
.
綜上可得:原不等式的解集為{x|﹣1<x<1};(2)令g(x)=f(x)+x,當x≤ ![]() 時,g(x)=|x﹣a|﹣x﹣1,由a
時,g(x)=|x﹣a|﹣x﹣1,由a ![]() ,
,
可得g(x)= 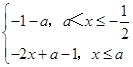 ,對于x∈
,對于x∈ ![]() ,
,
使得f(x)+x≥3恒成立.只需[g(x)]min≥3,x∈ ![]() ,
,
作出g(x)的圖象,可得:[g(x)]min=g(a)=﹣a﹣1,
∴﹣a﹣1≥3,可得a≤﹣4.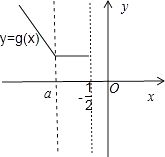
【解析】(1))令|2x+1|=0,解得x=﹣ ![]() ,令|x﹣2|=0,解得x=2.對x分類討論即可得出.(2)令g(x)=f(x)+x,當x≤
,令|x﹣2|=0,解得x=2.對x分類討論即可得出.(2)令g(x)=f(x)+x,當x≤ ![]() 時,g(x)=|x﹣a|﹣x﹣1,由a
時,g(x)=|x﹣a|﹣x﹣1,由a ![]() ,可得g(x)=
,可得g(x)= 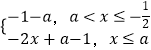 ,對于x∈
,對于x∈ ![]() ,使得f(x)+x≥3恒成立.只需[g(x)]min≥3,x∈
,使得f(x)+x≥3恒成立.只需[g(x)]min≥3,x∈ ![]() ,利用圖象,即可得出.
,利用圖象,即可得出.
【考點精析】本題主要考查了絕對值不等式的解法的相關知識點,需要掌握含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規律:關鍵是去掉絕對值的符號才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】定義:若對定義域內任意x,都有![]() (a為正常數),則稱函數
(a為正常數),則稱函數![]() 為“a距”增函數.
為“a距”增函數.
(1)若![]() ,
,![]() (0,
(0,![]() ),試判斷
),試判斷![]() 是否為“1距”增函數,并說明理由;
是否為“1距”增函數,并說明理由;
(2)若![]() ,
,![]() R是“a距”增函數,求a的取值范圍;
R是“a距”增函數,求a的取值范圍;
(3)若![]() ,
,![]() (﹣1,
(﹣1,![]() ),其中k
),其中k![]() R,且為“2距”增函數,求
R,且為“2距”增函數,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義域為
的定義域為![]() ,若存在閉區間
,若存在閉區間![]() ,使得函數
,使得函數![]() 滿足:①
滿足:①![]() 在
在![]() 上是單調函數;②
上是單調函數;②![]() 在
在![]() 上的值域是
上的值域是![]() ,則稱區間
,則稱區間![]() 是函數
是函數![]() 的“和諧區間”.下列結論錯誤的是( )
的“和諧區間”.下列結論錯誤的是( )
A. 函數![]() 存在“和諧區間”
存在“和諧區間”
B. 函數![]() 不存在“和諧區間”
不存在“和諧區間”
C. 函數![]() 存在“和諧區間”
存在“和諧區間”
D. 函數![]() (
(![]() 且
且![]() )不存在“和諧區間”
)不存在“和諧區間”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD,底面ABCD為菱形,PA⊥平面ABCD,∠ABC=60°,E,F分別是BC,PC的中點. (I)證明:AE⊥PD;
(II)H是PD上的動點,EH與平面PAD所成的最大角為45°,求二面角E﹣AF﹣C的正切值.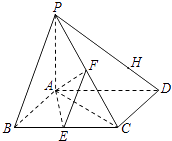
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB是圓O的直徑,弦CD⊥AB于點M,E是CD延長線上一點,AB=10,CD=8,3ED=4OM,EF切圓O于F,BF交CD于G. 
(1)求證:△EFG為等腰三角形;
(2)求線段MG的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() ,
,![]() ,則下列結論正確的是( )
,則下列結論正確的是( )
A. 把![]() 上所有的點向右平移
上所有的點向右平移![]() 個單位長度,再把所有圖象上各點的橫坐標縮短到原來的
個單位長度,再把所有圖象上各點的橫坐標縮短到原來的![]() 倍(縱坐標不變),得到曲線
倍(縱坐標不變),得到曲線![]()
B. 把![]() 上所有點向左平移
上所有點向左平移![]() 個單位長度,再把所得圖象上各點的橫坐標伸長到原來的3倍(縱坐標不變),得到曲線
個單位長度,再把所得圖象上各點的橫坐標伸長到原來的3倍(縱坐標不變),得到曲線![]()
C. 把![]() 上各點的橫坐標縮短到原來的
上各點的橫坐標縮短到原來的![]() 倍(縱坐標不變),再把所得圖象上所有的點向左平移
倍(縱坐標不變),再把所得圖象上所有的點向左平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]()
D. 把![]() 上各點的橫坐標伸長到原來的3倍(縱坐標不變),再把所得圖象上所有的點向左平移
上各點的橫坐標伸長到原來的3倍(縱坐標不變),再把所得圖象上所有的點向左平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解學生的課外閱讀時間情況,某學校隨機抽取了50人進行統計分析,把這50人每天閱讀的時間(單位:分鐘)繪制成頻數分布表,如下表所示:
閱讀時間 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120] |
人數 | 8 | 10 | 12 | 11 | 7 | 2 |
若把每天閱讀時間在60分鐘以上(含60分鐘)的同學稱為“閱讀達人”,根據統計結果中男女生閱讀達人的數據,制作出如圖所示的等高條形圖:

(1)根據已知條件完成2x2列聯表;
男生 | 女生 | 總計 | |
閱讀達人 | |||
非閱讀達人 | |||
總計 |
(2)并判斷是否有![]() 的把握認為“閱讀達人”跟性別有關?
的把握認為“閱讀達人”跟性別有關?
附:參考公式![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數,f(x)=|x﹣a|
(Ⅰ)當a=2,解不等式,f(x)≥5﹣|x﹣1|;
(Ⅱ)若f(x)≤1的解集為[0,2],![]() +
+![]() =a(m>0,n>0),求證:m+2n≥4.
=a(m>0,n>0),求證:m+2n≥4.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com