
【題目】如圖放置的邊長為1的正方形![]() 沿
沿![]() 軸滾動,點
軸滾動,點![]() 恰好經過原點.設頂點
恰好經過原點.設頂點![]() 的軌跡方程是
的軌跡方程是![]() ,則對函數
,則對函數![]() 有下列判斷:①函數
有下列判斷:①函數![]() 是偶函數;②對任意的
是偶函數;②對任意的![]() ,都有
,都有![]() ;③函數
;③函數![]() 在區間
在區間![]() 上單調遞減;④函數
上單調遞減;④函數![]() 的值域是
的值域是![]() ;⑤
;⑤![]() .其中判斷正確的序號是__________.
.其中判斷正確的序號是__________.

【答案】①②⑤
【解析】
根據正方形的運動,得到點P的軌跡方程,然后根據函數的圖象和性質分別進行判斷即可.
當﹣2≤x≤﹣1,P的軌跡是以A為圓心,半徑為1的![]() 圓,
圓,
當﹣1≤x≤1時,P的軌跡是以B為圓心,半徑為![]() 的
的![]() 圓,
圓,
當1≤x≤2時,P的軌跡是以C為圓心,半徑為1的![]() 圓,
圓,
當3≤x≤4時,P的軌跡是以A為圓心,半徑為1的![]() 圓,
圓,
∴函數的周期是4.
因此最終構成圖象如下:
①,根據圖象的對稱性可知函數y=f(x)是偶函數,故①正確;
②,由圖象即分析可知函數的周期是4.
即f(x+4)=f(x),即f(x+2)=f(x﹣2),故②正確;
③,函數y=f(x)在區間[2,3]上單調遞增,
故③錯誤;
④,由圖象可得f(x)的值域為[0,![]() ],故④錯誤;
],故④錯誤;
⑤,根據積分的幾何意義可知![]() f(x)dx
f(x)dx![]() π(
π(![]() )2
)2![]() 1×1
1×1![]() π×12
π×12![]() ,
,
故⑤正確.
故答案為:①②⑤.


科目:高中數學 來源: 題型:
【題目】為推動文明城市創建,提升城市整體形象,2018年12月30日鹽城市人民政府出臺了《鹽城市停車管理辦法》,2019年3月1日起施行.這項工作有利于市民養成良好的停車習慣,幫助他們樹立綠色出行的意識,受到了廣大市民的一致好評.現從某單位隨機抽取80名職工,統計了他們一周內路邊停車的時間![]() (單位:小時),整理得到數據分組及頻率分布直方圖如下:
(單位:小時),整理得到數據分組及頻率分布直方圖如下:

組號 | 分組 | 頻數 |
1 |
| 6 |
2 |
| 8 |
3 |
| 22 |
4 |
| 28 |
5 |
| 12 |
6 |
| 4 |
(1)從該單位隨機選取一名職工,試計算這名職工一周內路邊停車的時間少于8小時的頻率;
(2)求頻率分布直方圖中![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點
的兩個焦點![]() ,
,![]() ,且橢圓過點
,且橢圓過點![]() ,
,![]() ,且
,且![]() 是橢圓上位于第一象限的點,且
是橢圓上位于第一象限的點,且![]() 的面積
的面積![]() .
.
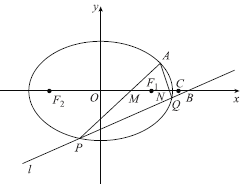
(1)求點![]() 的坐標;
的坐標;
(2)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于點
相交于點![]() ,
,![]() ,直線
,直線![]() ,
,![]() 與
與![]() 軸相交于
軸相交于![]() ,
,![]() 兩點,點
兩點,點![]() ,則
,則![]() 是否為定值,如果是定值,求出這個定值,如果不是請說明理由.
是否為定值,如果是定值,求出這個定值,如果不是請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,n∈N*.
,n∈N*.
(1)設f(x)=a0+a1x+a2x2+…+anxn,
①求a0+a1+a2+…+an;
②若在a0,a1,a2,…,an中,唯一的最大的數是a4,試求n的值;
(2)設f(x)=b0+b1(x+1)+b2(x+1)2+…+bn(x+1)n,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2012年12月18日,作為全國首批開展空氣質量新標準監測的74個城市之一,鄭州市正式發布![]() 數據.資料表明,近幾年來,鄭州市霧霾治理取得了很大成效,空氣質量與前幾年相比得到了很大改善.鄭州市設有9個監測站點監測空氣質量指數(
數據.資料表明,近幾年來,鄭州市霧霾治理取得了很大成效,空氣質量與前幾年相比得到了很大改善.鄭州市設有9個監測站點監測空氣質量指數(![]() ),其中在輕度污染區、中度污染區、重度污染區分別設有2,5,2個監測站點,以9個站點測得的
),其中在輕度污染區、中度污染區、重度污染區分別設有2,5,2個監測站點,以9個站點測得的![]() 的平均值為依據,播報我市的空氣質量.
的平均值為依據,播報我市的空氣質量.
(Ⅰ)若某日播報的![]() 為118,已知輕度污染區
為118,已知輕度污染區![]() 的平均值為74,中度污染區
的平均值為74,中度污染區![]() 的平均值為114,求重度污染區
的平均值為114,求重度污染區![]() 的平均值;
的平均值;
(Ⅱ)如圖是2018年11月的30天中![]() 的分布,11月份僅有一天
的分布,11月份僅有一天![]() 在
在![]() 內.
內.
組數 | 分組 | 天數 |
第一組 |
| 3 |
第二組 |
| 4 |
第三組 |
| 4 |
第四組 |
| 6 |
第五組 |
| 5 |
第六組 |
| 4 |
第七組 |
| 3 |
第八組 |
| 1 |
①鄭州市某中學利用每周日的時間進行社會實踐活動,以公布的![]() 為標準,如果
為標準,如果![]() 小于180,則去進行社會實踐活動.以統計數據中的頻率為概率,求該校周日進行社會實踐活動的概率;
小于180,則去進行社會實踐活動.以統計數據中的頻率為概率,求該校周日進行社會實踐活動的概率;
②在“創建文明城市”活動中,驗收小組把鄭州市的空氣質量作為一個評價指標,從當月的空氣質量監測數據中抽取3天的數據進行評價,設抽取到![]() 不小于180的天數為
不小于180的天數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,橢圓
上,橢圓![]() 的離心率是
的離心率是![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設點![]() 為橢圓長軸的左端點,
為橢圓長軸的左端點,![]() 為橢圓上異于橢圓
為橢圓上異于橢圓![]() 長軸端點的兩點,記直線
長軸端點的兩點,記直線![]() 斜率分別為
斜率分別為![]() ,若
,若![]() ,請判斷直線
,請判斷直線![]() 是否過定點?若過定點,求該定點坐標,若不過定點,請說明理由.
是否過定點?若過定點,求該定點坐標,若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1所示,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的平分線,點
的平分線,點![]() 在線段
在線段![]() 上,
上, ![]() .如圖2所示,將
.如圖2所示,將![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,連結
,連結![]() ,設點
,設點![]() 是
是![]() 的中點.
的中點.
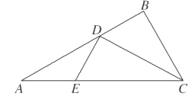

圖1 圖2
(1)求證: ![]() 平面
平面![]() ;
;
(2)在圖2中,若![]() 平面
平面![]() ,其中
,其中![]() 為直線
為直線![]() 與平面
與平面![]() 的交點,求三棱錐
的交點,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com