【題目】運行如圖所示的程序框圖，則輸出的結果是（ ） 
A.e2016﹣e2015
B.e2017﹣e2016
C.e2015﹣1
D.e2016﹣1
【答案】D
【解析】解：當n=1時，滿足繼續循環的條件，S=e﹣1，n=2，
當n=2時，滿足繼續循環的條件，S=e2﹣1，n=3，
當n=3時，滿足繼續循環的條件，S=e3﹣1，n=4，
…
當n=k時，滿足繼續循環的條件，S=ek﹣1，n=k+1，
…
當n=2016時，滿足繼續循環的條件，S=e2016﹣1，n=2017，
當n=2017時，不滿足繼續循環的條件，
故輸出的S值為：e2016﹣1，
故選：D
【考點精析】本題主要考查了程序框圖的相關知識點，需要掌握程序框圖又稱流程圖，是一種用規定的圖形、指向線及文字說明來準確、直觀地表示算法的圖形;一個程序框圖包括以下幾部分：表示相應操作的程序框；帶箭頭的流程線；程序框外必要文字說明才能正確解答此題．
科目：高中數學 來源： 題型：
【題目】某化肥廠生產甲、乙兩種混合肥料，需要A，B，C三種主要原料.生產1車皮甲種肥料和生產1車皮乙種肥料所需三種原料的噸數如下表所示：
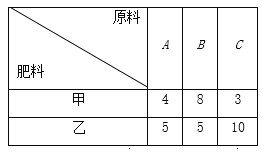
現有A種原料200噸，B種原料360噸，C種原料300噸.在此基礎上生產甲、乙兩種肥料.已知生產1車皮甲種肥料，產生的利潤為2萬元；生產1車皮乙種肥料，產生的利潤為3萬元.分別用x，y表示計劃生產甲、乙兩種肥料的車皮數.
(1)用x，y列出滿足生產條件的數學關系式，并畫出相應的平面區域；
(2)問分別生產甲、乙兩種肥料各多少車皮，能夠產生最大的利潤？并求出此最大利潤.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】f（x）是定義在（0，+∞）上單調函數，且對x∈（0，+∞），都有f（f（x）﹣lnx）=e+1，則方程f（x）﹣f′（x）=e的實數解所在的區間是（ ）
A.（0， 
）
B.（ ，1）
C.（1，e）
D.（e，3）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足a1+2a2+3a3+…+nan=n（n∈N*）．
（1）求數列{an}的通項公式an；
（2）令 
，寫出Tn關于n的表達式，并求滿足Tn＞ 
時n的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=2 
sin 
cos ﹣2sin2 （ω＞0）的最小正周期為3π．
（I）求函數f（x）的單調遞增區間；
（Ⅱ）在△ABC中，a，b，c分別為角A，B，C所對的邊，a＜b＜c， a=2csinA，并且f（ 
A+ 
）= 
，求cosB的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有一個同學家開了一個奶茶店，他為了研究氣溫對熱奶茶銷售杯數的影響，從一季度中隨機選取5天，統計出氣溫與熱奶茶銷售杯數，如表：
氣溫 | 0 | 4 | 12 | 19 | 27 |
熱奶茶銷售杯數 | 150 | 132 | 130 | 104 | 94 |
（Ⅰ）求熱奶茶銷售杯數關于氣溫的線性回歸方程
（
精確到0.1），若某天的氣溫為
，預測這天熱奶茶的銷售杯數；
（Ⅱ）從表中的5天中任取兩天，求所選取兩天中至少有一天熱奶茶銷售杯數大于130的概率．
參考數據：
，
.
參考公式：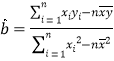
，
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地隨著經濟的發展，居民收入逐年增長，下表是該地一建設銀行連續五年的儲蓄存款（年底余額），如下表1：
為了研究計算的方便，工作人員將上表的數據進行了處理，
得到下表2：
（1）求
關于
的線性回歸方程；
（2）通過（1）中的方程，求出
關于
的回歸方程；
（3）用所求回歸方程預測到2010年年底，該地儲蓄存款額可達多少？
（附：對于線性回歸方程
，其中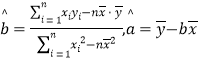
）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
