【題目】已知函數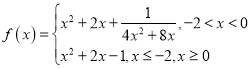
，若函數
有6個零點，則實數
的取值范圍是_________.
【答案】
【解析】
由題意首先研究函數
的性質，然后結合函數的性質數形結合得到關于a的不等式，求解不等式即可確定實數a的取值范圍.
當
時，函數
在區間
上單調遞增，
很明顯
，且存在唯一的實數
滿足
，
當
時，由對勾函數的性質可知函數
在區間
上單調遞減，在區間
上單調遞增，
結合復合函數的單調性可知函數
在區間
上單調遞減，在區間
上單調遞增，且當
時，
，
考查函數
在區間
上的性質，
由二次函數的性質可知函數在區間
上單調遞減，在區間
上單調遞增，
函數
有6個零點，即方程
有6個根，
也就是
有6個根，即
與
有6個不同交點，
注意到函數
關于直線
對稱，則函數關于直線對稱，
繪制函數的圖像如圖所示，
觀察可得：
，即
.
綜上可得，實數
的取值范圍是.
故答案為．
學練快車道快樂假期暑假作業新疆人民出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案
小學暑假作業東南大學出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目：高中數學 來源： 題型：
【題目】已知拋物線
，焦點為
，直線
交拋物線
于
兩點，
是線段
的中點，過作
軸的垂線交拋物線于點
.
（1）求拋物線的焦點坐標；
（2）若拋物線上有一點
到焦點的距離為
，求此時
的值；
（3）是否存在實數，使
是以為直角頂點的直角三角形？若存在，求出的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從4名男同學中選出2人，6名女同學中選出3人，并將選出的5人排成一排．
（1）共有多少種不同的排法？
（2）若選出的2名男同學不相鄰，共有多少種不同的排法？（用數字表示）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，橢圓
的參數方程為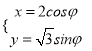
（
為參數），以原點
為極點， 
軸正半軸為極軸建立極坐標系，直線
的極坐標方程為
.
（1）求經過橢圓
右焦點
且與直線
垂直的直線的極坐標方程；
（2）若
為橢圓
上任意-點，當點
到直線
距離最小時，求點
的直角坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】近年來，隨著互聯網的發展，諸如“滴滴打車”“神州專車”等網約車服務在我國各：城市迅猛發展，為人們出行提供了便利，但也給城市交通管理帶來了一些困難.為掌握網約車在
省的發展情況，省某調查機構從該省抽取了
個城市，分別收集和分析了網約車的
兩項指標數
，數據如下表所示：
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
|
|
|
|
|
|
|
|
|
|
|
|
經計算得：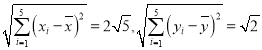
（1）試求
與
間的相關系數
，并利用說明與是否具有較強的線性相關關系(若
，則線性相關程度很高，可用線性回歸模型擬合)；
（2）立關于的回歸方程，并預測當
指標數為
時，
指標數的估計值.
附：相關公式：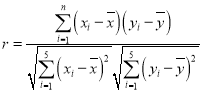
，
參考數據：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的右焦點為
，點
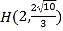在橢圓上．
（Ⅰ）求橢圓的方程；
（Ⅱ）點
在圓
上，且
在第一象限，過
作
的切線交橢圓于
兩點，問： 
的周長是否為定值？若是，求出定值；若不是，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】盒內有大小相同的9個球，其中2個紅色球，3個白色球，4個黑色球.規定取出1個紅色球得1分，取出1個白色球得0分，取出1個黑色球得
分，現從盒內任取3個球.
(Ⅰ)求取出的3個球中至少有一個紅球的概率；
(Ⅱ)求取出的3個球得分之和恰為1分的概率；
(Ⅲ)設
為取出的3個球中白色球的個數，求
的分布列及期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校從學生會宣傳部6名成員(其中男生4人，女生2人)中，任選3人參加某省舉辦的“我看中國改革開放三十年”演講比賽活動．
(1)設所選3人中女生人數為ξ，求ξ的分布列；
(2)求男生甲或女生乙被選中的概率；
(3)設“男生甲被選中”為事件A，“女生乙被選中”為事件B，求P(B)和P(B|A)．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
