【題目】畫糖人是一種以糖為材料在石板上進行造型的民間藝術(shù).某糖人師傅在公園內(nèi)畫糖人，每天賣出某種糖人的個數(shù)與價格相關(guān)，其相關(guān)數(shù)據(jù)統(tǒng)計如下表：
每個糖人的價格 | 9 | 10 | 11 | 12 | 13 |
賣出糖人的個數(shù) | 54 | 50 | 46 | 43 | 39 |
（1）根據(jù)表中數(shù)據(jù)求
關(guān)于
的回歸直線方程；
（2）若該種造型的糖人的成本為2元/個，為使糖人師傅每天獲得最大利潤，則該種糖人應(yīng)定價多少元？（精確到1元）
參考公式：回歸直線方程
，其中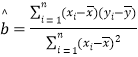
，
.
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）=
-x2+ef′（
）x．
（Ⅰ）求f（x）的單調(diào)區(qū)間；
（Ⅱ）若存在x1，x2（x1＜x2），使得f（x1）+f（x2）=1，求證：x1+x2＜2．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】為了研究某種細菌的繁殖個數(shù)y隨天數(shù)x的變化情況，收集數(shù)據(jù)如下：
天數(shù)x | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖個數(shù)y | 6 | 12 | 25 | 49 | 95 | 190 |
（1）根據(jù)散點圖，判斷
與
哪一個適合作為y關(guān)于x的回歸方程類型；（給出判斷即可，不用說明理由）
（2）根據(jù)（1）中的判斷及表中數(shù)據(jù)，求y關(guān)于x的回歸方程
參考數(shù)據(jù)：
，
，
，
，
，
參考公式：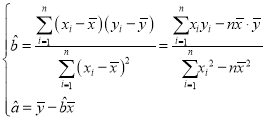
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在全面抗擊新冠肺炎疫情這一特殊時期，我市教育局提出“停課不停學”的口號，鼓勵學生線上學習.某校數(shù)學教師為了調(diào)查高三學生數(shù)學成績與線上學習時間之間的相關(guān)關(guān)系，對高三年級隨機選取45名學生進行跟蹤問卷，其中每周線上學習數(shù)學時間不少于5小時的有19人，余下的人中，在檢測考試中數(shù)學平均成績不足120分的占
，統(tǒng)計成績后得到如下
列聯(lián)表：
分數(shù)不少于120分 | 分數(shù)不足120分 | 合計 | |
線上學習時間不少于5小時 | 4 | 19 | |
線上學習時間不足5小時 | |||
合計 | 45 |
（1）請完成上面列聯(lián)表；并判斷是否有99%的把握認為“高三學生的數(shù)學成績與學生線上學習時間有關(guān)”；
（2）在上述樣本中從分數(shù)不少于120分的學生中，按照分層抽樣的方法，抽到線上學習時間不少于5小時和線上學習時間不足5小時的學生共5名，若在這5名學生中隨機抽取2人，求至少1人每周線上學習時間不足5小時的概率.
（下面的臨界值表供參考）
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（參考公式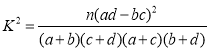
其中
）
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知圓周上有七個不同的點，以其中任意一點為始點，另一點為終點作向量，作出所有的向量（對于點
、
，若作出向量
，則不再作向量
）.若其中某四點所確定的凸四邊形的四條邊是首尾相接的四個向量，則稱其為“零四邊形”.試求以這七個點中四個點為頂點的凸四邊形中，零四邊形個數(shù)的最大值
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
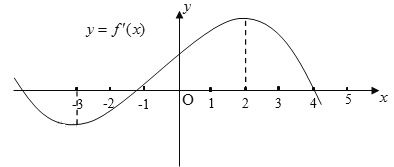
【題目】如果函數(shù)
的導(dǎo)函數(shù)
的圖象如圖所示，則以下關(guān)于函數(shù)的判斷：
①在區(qū)間
內(nèi)單調(diào)遞增；
②在區(qū)間
內(nèi)單調(diào)遞減；
③在區(qū)間
內(nèi)單調(diào)遞增；
④
是極小值點；
⑤
是極大值點.
其中正確的是（ ）
A. ③⑤B. ②③C. ①④⑤D. ①②④
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
，若關(guān)于
的方程
恰有兩個不相等的實數(shù)根， 則實數(shù)
的取值范圍是
A. 
B. 
，
C. 
，
D. ，
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知f（x）＝3x2－2x，數(shù)列{an}的前n項和為Sn，點（n，Sn）（n∈N*）均在函數(shù)y＝f（x）的圖象上．
（1）求數(shù)列{an}的通項公式；
（2）設(shè)bn＝
，Tn是數(shù)列{bn}的前n項和，求使得Tn<
對所有n∈N*都成立的最小正整數(shù)m．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
