
【題目】已知函數![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)若![]() ,
,![]() ,證明:
,證明:![]() .
.
【答案】(1)函數![]() 是
是![]() 上的減函數 ;(2)見解析.
上的減函數 ;(2)見解析.
【解析】
(1)求出函數f(x)的定義域,并對函數f(x)求導,確定f′(x)的正負,即可確定函數f(x)在定義域上的單調性;(2)設a>b>0,分為兩個不等式![]() 和
和![]() .證明不等式
.證明不等式![]() 時,轉化為
時,轉化為![]() ,換元t=
,換元t=![]() >1,轉化為
>1,轉化為![]() ,通過函數f(x)在區間(1,+∞)上的單調性來證明;證明不等式
,通過函數f(x)在區間(1,+∞)上的單調性來證明;證明不等式![]() ,轉化為
,轉化為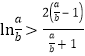 ,換元x=
,換元x=![]() >1,構造函數
>1,構造函數![]() ,通過函數g(x)在區間(1,+∞)的單調性來證明.
,通過函數g(x)在區間(1,+∞)的單調性來證明.
(1)函數f(x)的定義域為(0,+∞),![]() ,所以,函數f(x)在定義域(0,+∞)上單調遞減;
,所以,函數f(x)在定義域(0,+∞)上單調遞減;
(2)假設a>b>0.先證明不等式![]() ,即證
,即證![]() ,即證
,即證![]() ,令
,令![]() ,則原不等式即為
,則原不等式即為![]() ,其中t>1,由(1)知,函數f(x)在(0,+∞)上單調遞減,當t>1時,f(t)<f(1)=0,即
,其中t>1,由(1)知,函數f(x)在(0,+∞)上單調遞減,當t>1時,f(t)<f(1)=0,即
![]() ,即
,即![]() ,所以,當a>b>0時,
,所以,當a>b>0時,![]() .
.
下面證明![]() .即證
.即證![]() ,即
,即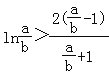 ,
,
令![]() ,即證
,即證![]() ,其中x>1,構造函數
,其中x>1,構造函數![]() ,其中x>1,
,其中x>1,![]() ,所以,函數g(x)在區間(1,+∞)上單調遞增,所以,g(x)>g(1)=0,所以,當x>1時,
,所以,函數g(x)在區間(1,+∞)上單調遞增,所以,g(x)>g(1)=0,所以,當x>1時,![]() ,
,
所以,當a>b>0時,![]() .
.
綜上所述,當a>0,b>0時,![]() .
.


科目:高中數學 來源: 題型:
【題目】橢圓![]() 的離心率為
的離心率為![]() ,其左焦點到點
,其左焦點到點![]() 的距離為
的距離為![]() ,不過原點O的直線
,不過原點O的直線![]() 與C交于A,B兩點,且線段AB被直線OP平分.
與C交于A,B兩點,且線段AB被直線OP平分.
(1)求橢圓C的方程;
(2)求k的值;
(3)求![]() 面積取最大值時直線l的方程.
面積取最大值時直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中學生研學旅行是通過集體旅行、集中食宿方式開展的研究性學習和旅行體驗相結合的校外教育活動,是學校教育和校外教育銜接的創新形式,是綜合實踐育人的有效途徑.每年暑期都會有大量中學生參加研學旅行活動.為了解某地區中學生暑期研學旅行支出情況,在該地區各個中學隨機抽取了部分中學生進行問卷調查,從中統計得到中學生暑期研學旅行支出(單位:百元)頻率分布直方圖如圖所示.

(1)利用分層抽樣在![]() ,
,![]() ,
,![]() 三組中抽取5人,應從這三組中各抽取幾人?
三組中抽取5人,應從這三組中各抽取幾人?
(2)從(1)抽取的5人中隨機選出2人,對其消費情況進行進一步分析,求這2人不在同一組的概率;
(3)假設同組中的每個數據都用該區間的左端點值代替,估計該地區中學生暑期研學旅行支出的平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學習雷鋒精神前半年內某單位餐廳的固定餐椅經常有損壞,學習雷鋒精神時全修好;單位對學習雷鋒精神前后各半年內餐椅的損壞情況作了一個大致統計,具體數據如表:
損壞餐椅數 | 未損壞餐椅數 | 總計 | |
學習雷鋒精神前 | 50 | 150 | 200 |
學習雷鋒精神后 | 30 | 170 | 200 |
總計 | 80 | 320 | 400 |
![]() 求:學習雷鋒精神前后餐椅損壞的百分比分別是多少?并初步判斷損毀餐椅數量與學習雷鋒精神是否有關?
求:學習雷鋒精神前后餐椅損壞的百分比分別是多少?并初步判斷損毀餐椅數量與學習雷鋒精神是否有關?
![]() 請說明是否有
請說明是否有![]() 以上的把握認為損毀餐椅數量與學習雷鋒精神
以上的把握認為損毀餐椅數量與學習雷鋒精神
有關?![]() 參考公式:
參考公式:![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知點
中,已知點![]() 和
和![]() .
.
(![]() )若
)若![]() ,
, ![]() 是正方形一條邊上的兩個頂點,求這個正方形過頂點
是正方形一條邊上的兩個頂點,求這個正方形過頂點![]() 的兩條邊所在直線的方程;
的兩條邊所在直線的方程;
(![]() )若
)若![]() ,
, ![]() 是正方形一條對角線上的兩個頂點,求這個正方形另外一條對角線所在直線的方程及其端點的坐標.
是正方形一條對角線上的兩個頂點,求這個正方形另外一條對角線所在直線的方程及其端點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某觀光海域AB段的長度為3百公里,一超級快艇在AB段航行,經過多次試驗得到其每小時航行費用Q(單位:萬元)與速度v(單位:百公里/小時)(0≤v≤3)的以下數據:
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
為描述該超級快艇每小時航行費用Q與速度v的關系,現有以下三種函數模型供選擇:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)試從中確定最符合實際的函數模型,并求出相應的函數解析式;
(2)該超級快艇應以多大速度航行才能使AB段的航行費用最少?并求出最少航行費用.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com