
【題目】甲乙兩地相距![]() ,貨車(chē)從甲地勻速行駛到乙地,速度不得超過(guò)
,貨車(chē)從甲地勻速行駛到乙地,速度不得超過(guò)![]() ,已知貨車(chē)每小時(shí)的運(yùn)輸成本(單位:圓)由可變本和固定組成組成,可變成本是速度平方的
,已知貨車(chē)每小時(shí)的運(yùn)輸成本(單位:圓)由可變本和固定組成組成,可變成本是速度平方的![]() 倍,固定成本為
倍,固定成本為![]() 元.
元.
(1)將全程勻速勻速成本![]() (元)表示為速度
(元)表示為速度![]() 的函數(shù),并指出這個(gè)函數(shù)的定義域;
的函數(shù),并指出這個(gè)函數(shù)的定義域;
(2)若![]() ,為了使全程運(yùn)輸成本最小,貨車(chē)應(yīng)以多大的速度行駛?
,為了使全程運(yùn)輸成本最小,貨車(chē)應(yīng)以多大的速度行駛?
【答案】(1) ![]() ,定義域?yàn)?/span>
,定義域?yàn)?/span>![]() .(2)當(dāng)貨車(chē)以
.(2)當(dāng)貨車(chē)以![]() 的速度行駛,全程運(yùn)輸成本最小.
的速度行駛,全程運(yùn)輸成本最小.
【解析】試題分析:(1)求出汽車(chē)從甲地勻速行駛到乙地所用時(shí)間,根據(jù)貨車(chē)每小時(shí)的運(yùn)輸成本(以元為單位)由可變部分和固定部分組成,可得全程運(yùn)輸成本,及函數(shù)的定義域;
(2)利用基本不等式![]() 可得結(jié)論.
可得結(jié)論.
試題解析:
(1)可變成本為![]() ,固定成本為
,固定成本為![]() 元,所用時(shí)間為
元,所用時(shí)間為![]() ,
,
所以![]() ,即
,即![]() ,定義域?yàn)?/span>
,定義域?yàn)?/span>![]() .
.
(2)![]() ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)![]() ,即
,即![]() 時(shí),等號(hào)成立,
時(shí),等號(hào)成立,
所以當(dāng)![]() 時(shí),
時(shí), ![]() ,
,
答:當(dāng)貨車(chē)以![]() 的速度行駛,全程運(yùn)輸成本最小.
的速度行駛,全程運(yùn)輸成本最小.


 53天天練系列答案
53天天練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某小型企業(yè)甲產(chǎn)品生產(chǎn)的投入成本![]() (單位:萬(wàn)元)與產(chǎn)品銷(xiāo)售收入
(單位:萬(wàn)元)與產(chǎn)品銷(xiāo)售收入![]() (單位:萬(wàn)元)存在較好的線性關(guān)系,下表記錄了最近5次產(chǎn)品的相關(guān)數(shù)據(jù).
(單位:萬(wàn)元)存在較好的線性關(guān)系,下表記錄了最近5次產(chǎn)品的相關(guān)數(shù)據(jù).
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
(1)求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程;
的線性回歸方程;
(2)根據(jù)(1)中的回歸方程,判斷該企業(yè)甲產(chǎn)品投入成本20萬(wàn)元的毛利率更大還是投入成本24萬(wàn)元的毛利率更大(![]() )?
)?
相關(guān)公式: 
 ,
, ![]() .
.
【答案】(1)![]() .(2)投入成本20萬(wàn)元的毛利率更大.
.(2)投入成本20萬(wàn)元的毛利率更大.
【解析】試題分析:(1)由回歸公式,解得線性回歸方程為![]() ;(2)當(dāng)
;(2)當(dāng)![]() 時(shí),
時(shí), ![]() ,對(duì)應(yīng)的毛利率為
,對(duì)應(yīng)的毛利率為![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí), ![]() ,對(duì)應(yīng)的毛利率為
,對(duì)應(yīng)的毛利率為![]() ,故投入成本20萬(wàn)元的毛利率更大。
,故投入成本20萬(wàn)元的毛利率更大。
試題解析:
(1)![]() ,
, ![]() ,
,

![]() ,
, ![]() ,故
,故![]() 關(guān)于
關(guān)于![]() 的線性回歸方程為
的線性回歸方程為![]() .
.
(2)當(dāng)![]() 時(shí),
時(shí), ![]() ,對(duì)應(yīng)的毛利率為
,對(duì)應(yīng)的毛利率為![]() ,
,
當(dāng)![]() 時(shí),
時(shí), ![]() ,對(duì)應(yīng)的毛利率為
,對(duì)應(yīng)的毛利率為![]() ,
,
故投入成本20萬(wàn)元的毛利率更大.
【題型】解答題
【結(jié)束】
21
【題目】如圖,在正方體![]() 中,
中, ![]() 分別是棱
分別是棱![]() 的中點(diǎn),
的中點(diǎn), ![]() 為棱
為棱![]() 上一點(diǎn),且異面直線
上一點(diǎn),且異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() .
.

(1)證明: ![]() 為
為![]() 的中點(diǎn);
的中點(diǎn);
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法中不正確的序號(hào)為____________.
①若函數(shù)![]() 在
在![]() 上單調(diào)遞減,則實(shí)數(shù)
上單調(diào)遞減,則實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]() ;
;
②函數(shù)![]() 是偶函數(shù),但不是奇函數(shù);
是偶函數(shù),但不是奇函數(shù);
③已知函數(shù)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,則函數(shù)
,則函數(shù)![]() 的定義域是
的定義域是![]() ;
;
④若函數(shù)![]() 在
在![]() 上有最小值-4,(
上有最小值-4,(![]() ,
,![]() 為非零常數(shù)),則函數(shù)
為非零常數(shù)),則函數(shù)![]() 在
在![]() 上有最大值6.
上有最大值6.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 是實(shí)數(shù)集
是實(shí)數(shù)集![]() 上的奇函數(shù),求
上的奇函數(shù),求![]() 的值;
的值;
(2)用定義證明![]() 在實(shí)數(shù)集
在實(shí)數(shù)集![]() 上的單調(diào)遞增;
上的單調(diào)遞增;
(3)若![]() 的值域?yàn)?/span>
的值域?yàn)?/span>![]() ,且[
,且[![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)f(x)=x3+mlog2(x+ ![]() )(m∈R,m>0),則不等式f(m)+f(m2﹣2)≥0的解是 . (注:填寫(xiě)m的取值范圍)
)(m∈R,m>0),則不等式f(m)+f(m2﹣2)≥0的解是 . (注:填寫(xiě)m的取值范圍)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 。
。
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 在
在![]() 上的最大值;
上的最大值;
(2)若函數(shù)![]() 在
在![]() 處有極小值,求實(shí)數(shù)
處有極小值,求實(shí)數(shù)![]() 的值。
的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
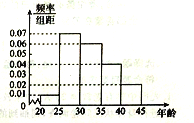
【題目】某市為了創(chuàng)建全國(guó)文明城市,面向社會(huì)招募志愿者,現(xiàn)從20歲至50歲的志愿者中按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示,若用分層抽樣的方法從這些志愿者中抽取20人參加“創(chuàng)建全國(guó)文明城市驗(yàn)收日”的活動(dòng)。
,得到的頻率分布直方圖如圖所示,若用分層抽樣的方法從這些志愿者中抽取20人參加“創(chuàng)建全國(guó)文明城市驗(yàn)收日”的活動(dòng)。
(1)求從第2組和第3組中抽取的人數(shù)分別是多少;
(2)若小李和小王都是32歲,同時(shí)參加了“創(chuàng)建全國(guó)文明城市驗(yàn)收日”的活動(dòng),現(xiàn)要從第3組抽取的人中臨時(shí)抽調(diào)兩人去執(zhí)行另一任務(wù),求小李和小王至少有一人被抽調(diào)的概率。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,點(diǎn)E、F分別在棱BB1、CC1上,且BE= ![]() BB1 , C1F=
BB1 , C1F= ![]() CC1 .
CC1 . 
(1)求平面AEF與平面ABC所成角α的余弦值;
(2)若G為BC的中點(diǎn),A1G與平面AEF交于H,且設(shè) ![]() =
= ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,角A,B,C所對(duì)的邊分別為a,b,c,( ![]() a﹣sinC)cosB=sinBcosC,b=4
a﹣sinC)cosB=sinBcosC,b=4 ![]() .
. 
(1)求角B的大小;
(2)D為BC邊上一點(diǎn),若AD=2,S△DAC=2 ![]() ,求DC的長(zhǎng).
,求DC的長(zhǎng).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com