
【題目】已知點![]() 在同一個球的球面上,
在同一個球的球面上,![]() ,
,![]() ,
,![]() .若四面體
.若四面體![]() 體積的最大值為
體積的最大值為![]() ,則這個球的表面積為_____.
,則這個球的表面積為_____.
【答案】![]()
【解析】
根據幾何體的特征,小圓的圓心為Q,若四面體ABCD的體積的最大值,由于底面積S△ABC不變,高最大時體積最大,可得DQ與面ABC垂直時體積最大,從而求出球的半徑,即可求出球的表面積.
根據題意知,A、B、C三點均在球心O的表面上,
且![]() ,
,![]() ,
,![]() ,由余弦定理可得BC
,由余弦定理可得BC![]() ,∴△ABC為直角三角形,
,∴△ABC為直角三角形,
∴△ABC外接圓直徑2r=AC=6,即r=3,
且S△ABC![]() ×3
×3![]() ,
,
AC的中點即為小圓的圓心設為Q,若四面體ABCD的體積的最大值,由于底面積S△ABC不變,高最大時體積最大,
所以,DQ與面ABC垂直時體積最大,最大值為![]() S△ABC×DQ
S△ABC×DQ![]() ,
,
∴DQ=3![]() ,
,
設球的半徑為R,則
在直角△AQO中,OA2=AQ2+OQ2,即R2=32+(3![]() ﹣R)2,∴R
﹣R)2,∴R![]() ,
,
∴球的表面積為![]() ,
,
故答案為![]() .
.


科目:高中數學 來源: 題型:
【題目】2012年,在“雜交水稻之父”袁隆平的實驗田內種植了![]() ,
,![]() 兩個品種的水稻,為了篩選出更優的品種,在
兩個品種的水稻,為了篩選出更優的品種,在![]() ,
,![]() 兩個品種的實驗田中分別抽取7塊實驗田,如圖所示的莖葉圖記錄了這14塊實驗田的畝產量(單位:
兩個品種的實驗田中分別抽取7塊實驗田,如圖所示的莖葉圖記錄了這14塊實驗田的畝產量(單位:![]() ),通過莖葉圖比較兩個品種的均值及方差,并從中挑選一個品種進行以后的推廣,有如下結論:①
),通過莖葉圖比較兩個品種的均值及方差,并從中挑選一個品種進行以后的推廣,有如下結論:①![]() 品種水稻的平均產量高于
品種水稻的平均產量高于![]() 品種水稻,推廣
品種水稻,推廣![]() 品種水稻;②
品種水稻;②![]() 品種水稻的平均產量高于
品種水稻的平均產量高于![]() 品種水稻,推廣
品種水稻,推廣![]() 品種水稻;③
品種水稻;③![]() 品種水稻比
品種水稻比![]() 品種水稻產量更穩定,推廣
品種水稻產量更穩定,推廣![]() 品種水稻;④
品種水稻;④![]() 品種水稻比
品種水稻比![]() 品種水稻產量更穩定,推廣
品種水稻產量更穩定,推廣![]() 品種水稻;其中正確結論的編號為( )
品種水稻;其中正確結論的編號為( )

A.①②B.①③C.②④D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓C:![]() 的一個頂點與拋物線:
的一個頂點與拋物線:![]() 的焦點重合,
的焦點重合,![]() 分別是橢圓的左、右焦點,離心率
分別是橢圓的左、右焦點,離心率![]() ,過橢圓右焦點
,過橢圓右焦點![]() 的直線l與橢圓C交于M、N兩點.
的直線l與橢圓C交于M、N兩點.
(1)求橢圓C的方程;
(2)是否存在直線l,使得![]() ,若存在,求出直線l的方程;若不存在,說明理由;
,若存在,求出直線l的方程;若不存在,說明理由;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在意大利,有一座滿是“斗笠”的灰白小鎮阿爾貝羅貝洛(Alberobello),這些圓錐形屋頂的奇特小屋名叫Trullo,于1996年被收入世界文化遺產名錄(如圖1).現測量一個屋頂,得到圓錐SO的底面直徑AB長為12m,母線SA長為18m(如圖2).C,D是母線SA的兩個三等分點(點D靠近點A),E是母線SB的中點.

(1)從點A到點C繞屋頂側面一周安裝燈光帶,求燈光帶的最小長度;
(2)現對屋頂進行加固,在底面直徑AB上某一點P,向點D和點E分別引直線型鋼管PD和PE.試確定點P的位置,使得鋼管總長度最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年4月23日“世界讀書日”來臨之際,某校為了了解中學生課外閱讀情況,隨機抽取了100名學生,并獲得了他們一周課外閱讀時間(單位:小時)的數據,按閱讀時間分組:第一組[0,5), 第二組[5,10),第三組[10,15),第四組[15,20),第五組[20,25],繪制了頻率分布直方圖如下圖所示。已知第三組的頻數是第五組頻數的3倍。
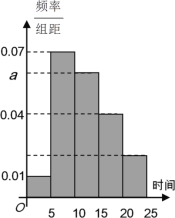
(1)求![]() 的值,并根據頻率分布直方圖估計該校學生一周課外閱讀時間的平均值;
的值,并根據頻率分布直方圖估計該校學生一周課外閱讀時間的平均值;
(2)現從第三、四、五這3組中用分層抽樣的方法抽取6人參加校“中華詩詞比賽”。經過比賽后,從這6人中隨機挑選2人組成該校代表隊,求這2人來自不同組別的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知一個八面體的各條棱長均為![]() ,四邊形
,四邊形![]() 為正方形,給出下列命題:
為正方形,給出下列命題:

①不平行的兩條棱所在的直線所成的角是![]() 或
或![]() ; ②四邊形
; ②四邊形![]() 是正方形;
是正方形;
③點![]() 到平面
到平面![]() 的距離為
的距離為![]() ; ④平面
; ④平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值為
所成的銳二面角的余弦值為![]() .
.
其中正確的命題全部序號為_________________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】詹姆斯·哈登(James Harden)是美國NBA當紅球星,自2012年10月加盟休斯頓火箭隊以來,逐漸成長為球隊的領袖.2017-18賽季哈登當選常規賽MVP(最有價值球員).
年份 | 2012-13 | 2013-14 | 2014-15 | 2015-16 | 2016-17 | 2017-18 |
年份代碼t | 1 | 2 | 3 | 4 | 5 | 6 |
常規賽場均得分y | 25.9 | 25.4 | 27.4 | 29.0 | 29.1 | 30.4 |
(Ⅰ)根據表中數據,求y關于t的線性回歸方程![]() (
(![]() ,
,![]()
![]() *);
*);
(Ⅱ)根據線性回歸方程預測哈登在2019-20賽季常規賽場均得分.
(附)對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:![]() ,
,![]()
(參考數據![]() ,計算結果保留小數點后一位)
,計算結果保留小數點后一位)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com