
【題目】已知函數![]() (
(![]() 為常數,
為常數, ![]() 為自然對數的底數).
為自然對數的底數).
(Ⅰ)當![]() 時,討論函數
時,討論函數![]() 在區間
在區間![]() 上極值點的個數;
上極值點的個數;
(Ⅱ)當![]() ,
, ![]() 時,對任意的
時,對任意的![]() 都有
都有![]() 成立,求正實數
成立,求正實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析(2)![]()
【解析】試題分析:(Ⅰ)第一步求函數的導數,第二步再設![]() ,并且求
,并且求![]() 以及
以及![]() 時,
時, ![]() ,分析函數
,分析函數![]() 的單調性,得到函數
的單調性,得到函數![]() 的取值范圍,并且根據
的取值范圍,并且根據![]() ,討論
,討論![]() 和函數
和函數![]() 的極值以及端點值的大小關系,得到函數
的極值以及端點值的大小關系,得到函數![]() 的極值點的個數;(Ⅱ)不等式等價于
的極值點的個數;(Ⅱ)不等式等價于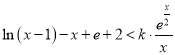 ,求
,求![]() 的最大值小于
的最大值小于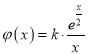 的最小值,即求得
的最小值,即求得![]() 的取得范圍.
的取得范圍.
試題解析:(Ⅰ) ![]() 時,
時, ![]() ,記
,記![]() ,
,
則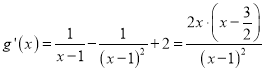 ,
, ![]() ,
,
當![]() 時,
時, ![]() ,
, ![]() 時,
時, ![]()
![]() ,
,
所以當![]() 時,
時, ![]() 取得極小值
取得極小值![]() ,又
,又![]() ,
, ![]() ,
,
![]() ,所以
,所以
(ⅰ)當![]() ,即
,即![]() 時,
時, ![]() ,函數
,函數![]() 在區間
在區間![]() 上無極值點;
上無極值點;
(ⅱ)當![]() 即
即![]() 時,
時, ![]() 有兩不同解,
有兩不同解,
函數![]() 在區間
在區間![]() 上有兩個極值點;
上有兩個極值點;
(ⅲ)當![]() 即
即![]() 時,
時, ![]() 有一解,
有一解,
函數![]() 在區間
在區間![]() 上有一個極值點;
上有一個極值點;
(ⅳ)當![]() 即
即![]() 時,
時, ![]() ,函數
,函數![]() 在區間
在區間![]() 上
上
無極值點;
(Ⅱ)當![]() 時,對任意的
時,對任意的![]() 都有
都有![]() ,
,
即![]() ,即
,即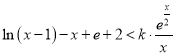
記![]() ,
, 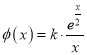 ,
,
由![]() ,當
,當![]() 時
時![]() ,
, ![]() 時,
時, ![]() ,
,
所以當![]() 時,
時, ![]() 取得最大值
取得最大值![]() ,
,
又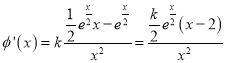 ,當
,當![]() 時
時![]() ,
, ![]() 時,
時, ![]() ,
,
所以當![]() 時,
時, ![]() 取得最小值
取得最小值![]() ,
,
所以只需要![]()
![]() ,即正實數
,即正實數![]() 的取值范圍是
的取值范圍是![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知數列![]() ,
, ![]() 都是單調遞增數列,若將這兩個數列的項按由小到大的順序排成一列(相同的項視為一項),則得到一個新數列
都是單調遞增數列,若將這兩個數列的項按由小到大的順序排成一列(相同的項視為一項),則得到一個新數列![]() .
.
(1)設數列![]() 、
、![]() 分別為等差、等比數列,若
分別為等差、等比數列,若![]() ,
, ![]() ,
, ![]() ,求
,求![]() ;
;
(2)設![]() 的首項為1,各項為正整數,
的首項為1,各項為正整數, ![]() ,若新數列
,若新數列![]() 是等差數列,求數列
是等差數列,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)設![]() (
(![]() 是不小于2的正整數),
是不小于2的正整數),![]() ,是否存在等差數列
,是否存在等差數列![]() ,使得對任意的
,使得對任意的![]() ,在
,在![]() 與
與![]() 之間數列
之間數列![]() 的項數總是
的項數總是![]() ?若存在,請給出一個滿足題意的等差數列
?若存在,請給出一個滿足題意的等差數列![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
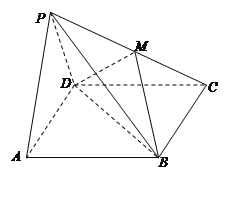
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 底面
底面![]() ,且
,且![]() 是邊長為
是邊長為![]() 的等邊三角形,
的等邊三角形, ![]() ,
, ![]() 在
在![]() 上,且
上,且![]() ∥面BDM.
∥面BDM.
(1)求直線PC與平面BDM所成角的正弦值;
(2)求平面BDM與平面PAD所成銳二面角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,函數f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤![]() )的部分圖象,其圖象與y軸交于點(0,
)的部分圖象,其圖象與y軸交于點(0,![]() )
)
(Ⅰ)求函數的解析式;
(Ⅱ)若![]() , 求
, 求![]() -
-![]() 的值.
的值.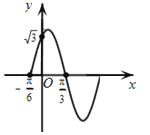
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=![]() , g(x)是二次函數,若f(g(x))的值域是[0,+∞),則函數g(x)的值域是( )
, g(x)是二次函數,若f(g(x))的值域是[0,+∞),則函數g(x)的值域是( )
A.(﹣∞,﹣1]∪[1,+∞)
B.(﹣∞,﹣1]∪[0,+∞)
C.[0,+∞)
D.[1,+∞)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com