
【題目】已知拋物線![]() 過點
過點![]() ,
,![]() 是拋物線
是拋物線![]() 上不同兩點,且
上不同兩點,且![]() (其中
(其中![]() 是坐標(biāo)原點),直線
是坐標(biāo)原點),直線![]() 與
與![]() 交于點
交于點![]() ,線段
,線段![]() 的中點為
的中點為![]() .
.
(Ⅰ)求拋物線![]() 的準(zhǔn)線方程;
的準(zhǔn)線方程;
(Ⅱ)求證:直線![]() 與
與![]() 軸平行.
軸平行.
【答案】(1) ![]() .(2)見解析.
.(2)見解析.
【解析】
(Ⅰ)把點代入即可求出p的值,可得拋物線C的準(zhǔn)線方程,
(Ⅱ)由題意可設(shè)直線AB的方程為y=x+m,設(shè)A(x1,y1),B(x2,y2),由題意可得y1+y2=2,即可求出點Q的縱坐標(biāo),再分別求出直線OA,BM的方程,求出點P的縱坐標(biāo),即可證明.
(Ⅰ)由題意得![]() ,解得
,解得![]() .
.
所以拋物線![]() 的準(zhǔn)線方程為
的準(zhǔn)線方程為![]() .
.
(Ⅱ)設(shè)![]() ,
,![]() ,
,
由![]() 得
得![]() ,則
,則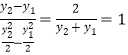 ,所以
,所以![]() .
.
所以線段![]() 中點
中點![]() 的為縱坐標(biāo)
的為縱坐標(biāo)![]() .
.
直線![]() 方程為
方程為 ┅①
┅①
直線![]() 方程為
方程為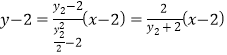 ┅②
┅②
聯(lián)立①②解得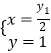 ,即點
,即點![]() 的為縱坐標(biāo)
的為縱坐標(biāo)![]() .
.
如果直線![]() 斜率不存在,結(jié)論也顯然成立.
斜率不存在,結(jié)論也顯然成立.



科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C:![]() 的焦距為2
的焦距為2![]() ,左頂點與上頂點連線的斜率為
,左頂點與上頂點連線的斜率為![]() .
.
(Ⅰ)求橢圓C的標(biāo)準(zhǔn)方程;
(Ⅱ)過點P(m,0)作圓x2+y2=1的一條切線l交橢圓C于M,N兩點,當(dāng)|MN|的值最大時,求m的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形![]() 是梯形,四邊形
是梯形,四邊形![]() 是矩形,且平面
是矩形,且平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是線段
是線段![]() 上的動點.
上的動點.
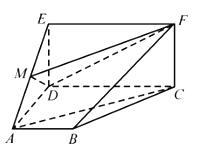
(1)試確定點![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并說明理由;
,并說明理由;
(2)在(1)的條件下,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,
,![]() .
.
(Ⅰ)當(dāng)![]() 時,求曲線
時,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(Ⅱ)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅲ)設(shè)![]() ,若對于任意
,若對于任意![]() ,總存在
,總存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}滿足:a1+a2+a3+…+an=n-an,(n=1,2,3,…)
(Ⅰ)求證:數(shù)列{an-1}是等比數(shù)列;
(Ⅱ)令bn=(2-n)(an-1)(n=1,2,3,…),如果對任意n∈N*,都有bn+![]() t≤t2,求實數(shù)t的取值范圍.
t≤t2,求實數(shù)t的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點![]() 是單位正方體
是單位正方體![]() 的對角面
的對角面![]() 上的一動點,過點
上的一動點,過點![]() 作垂直于平面
作垂直于平面![]() 的直線,與正方體的側(cè)面相交于
的直線,與正方體的側(cè)面相交于![]() 、
、![]() 兩點,則
兩點,則![]() 的面積的最大值為( )
的面積的最大值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了打好“精準(zhǔn)扶貧攻堅戰(zhàn)”某村扶貧書記打算帶領(lǐng)該村農(nóng)民種植新品種蔬菜,可選擇的種植量有三種:大量種植,適量種植,少量種植.根據(jù)收集到的市場信息,得到該地區(qū)該品種蔬菜年銷量頻率分布直方圖如圖,然后,該扶貧書記同時調(diào)查了同類其他地區(qū)農(nóng)民以往在各種情況下的平均收入如表1(表中收入單位:萬元):
表1
銷量 種植量 | 好 | 中 | 差 |
大量 |
| 8 | -4 |
適量 | 9 | 7 | 0 |
少量 | 4 | 4 | 2 |
但表格中有一格數(shù)據(jù)被墨跡污損,好在當(dāng)時調(diào)查的數(shù)據(jù)頻數(shù)分布表還在,其中大量種植的100戶農(nóng)民在市場銷量好的情況下收入情況如表2:
收入(萬元) | 11 | 11.5 | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 |
頻數(shù)(戶) | 5 | 10 | 15 | 10 | 15 | 20 | 10 | 10 | 5 |
(Ⅰ)根據(jù)題中所給數(shù)據(jù),請估計在市場銷量好的情況下,大量種植的農(nóng)民每戶的預(yù)期收益.(用以往平均收入來估計);
(Ⅱ)若該地區(qū)年銷量在10千噸以下表示銷量差,在10千噸至30千噸之間表示銷量中,在30千噸以上表示銷量好,試根據(jù)頻率分布直方圖計算銷量分別為好、中、差的概率(以頻率代替概率);
(Ⅲ)如果你是這位扶貧書記,請根據(jù)(Ⅰ)(Ⅱ),從農(nóng)民預(yù)期收益的角度分析,你應(yīng)該選擇哪一種種植量.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知兩定點![]() ,
,![]() ,點P是平面內(nèi)的動點,且
,點P是平面內(nèi)的動點,且![]() ,記動點P的軌跡W.
,記動點P的軌跡W.
(1)求動點P的軌跡W的方程;
(2)過點![]() 作兩條相垂直的直線分別交軌跡于G,H,M,N四點.設(shè)四邊形GMHN面積為S,求
作兩條相垂直的直線分別交軌跡于G,H,M,N四點.設(shè)四邊形GMHN面積為S,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com