
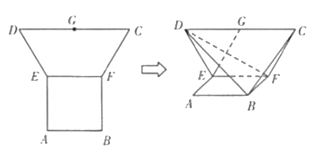
【題目】在平面多邊形![]() 中,四邊形
中,四邊形![]() 是邊長為2的正方形,四邊形
是邊長為2的正方形,四邊形![]() 為等腰梯形,
為等腰梯形,![]() 為
為![]() 的中點,
的中點,![]() ,現(xiàn)將梯形
,現(xiàn)將梯形![]() 沿
沿![]() 折疊,使平面
折疊,使平面![]() 平面
平面![]() .
.
(1)求證:![]() 面
面![]() ;
;
(2)求![]() 與平面
與平面![]() 成角的正弦值.
成角的正弦值.
 亮點激活精編提優(yōu)100分大試卷系列答案
亮點激活精編提優(yōu)100分大試卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點為別為
的左、右焦點為別為![]() 、
、![]() ,且過點
,且過點![]() 和
和![]() .
.
(1)求橢圓的標準方程;
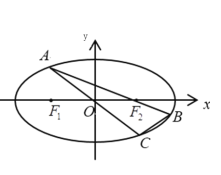
(2)如圖,點![]() 為橢圓上一動點(非長軸端點),
為橢圓上一動點(非長軸端點),![]() 的延長線與橢圓交于點
的延長線與橢圓交于點![]() ,
,![]() 的延長線與橢圓交于點
的延長線與橢圓交于點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)當![]() 時,判斷
時,判斷![]() 是否是函數(shù)
是否是函數(shù)![]() 的極值點,并說明理由;
的極值點,并說明理由;
(2)當![]() 時,不等式
時,不等式![]() 恒成立,求整數(shù)
恒成立,求整數(shù)![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】正項數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,且
,且![]() ,
,![]() (
(![]() 為常數(shù)).
為常數(shù)).
(1)求證:數(shù)列![]() 為等比數(shù)列;
為等比數(shù)列;
(2)若![]() ,且
,且![]() ,對任意
,對任意![]() ,
,![]() 都有
都有![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,是否存在正整數(shù)
,是否存在正整數(shù)![]() ,且
,且![]() ,使得
,使得![]() ,
,![]() ,
,![]() 三項成等比數(shù)列?
三項成等比數(shù)列?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() ,其中
,其中![]() .
.
(1)若![]() 滿足
滿足![]() .
.
①當![]() ,且
,且![]() 時,求
時,求![]() 的值;
的值;
②若存在互不相等的正整數(shù)![]() ,滿足
,滿足![]() ,且
,且![]() 成等差數(shù)列,求
成等差數(shù)列,求![]() 的值.
的值.
(2)設數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,數(shù)列
,數(shù)列![]() 的前n項和為
的前n項和為![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,且
,且![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設點P是直線![]() 上一點,過點P分別作拋物線
上一點,過點P分別作拋物線![]() 的兩條切線
的兩條切線![]() ,其中A、B為切點.
,其中A、B為切點.
(1)若點A的坐標為![]() ,求點P的橫坐標;
,求點P的橫坐標;
(2)當![]() 的面積為
的面積為![]() 時,求
時,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2019年7月,中國良渚古城遺址獲準列入世界遺產(chǎn)名錄,標志著中華五千年文明史得到國際社會認可.良渚古城遺址是人類早期城市文明的范例,實證了中華五千年文明史.考古科學家在測定遺址年齡的過程中利用了“放射性物質(zhì)因衰變而減少”這一規(guī)律.已知樣本中碳14的質(zhì)量N隨時間T(單位:年)的衰變規(guī)律滿足![]() (
(![]() 表示碳14原有的質(zhì)量),則經(jīng)過5730年后,碳14的質(zhì)量變?yōu)樵瓉淼?/span>______;經(jīng)過測定,良渚古城遺址文物樣本中碳14的質(zhì)量是原來的
表示碳14原有的質(zhì)量),則經(jīng)過5730年后,碳14的質(zhì)量變?yōu)樵瓉淼?/span>______;經(jīng)過測定,良渚古城遺址文物樣本中碳14的質(zhì)量是原來的![]() 至
至![]() ,據(jù)此推測良渚古城存在的時期距今約在5730年到______年之間.(參考數(shù)據(jù):
,據(jù)此推測良渚古城存在的時期距今約在5730年到______年之間.(參考數(shù)據(jù):![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知橢圓![]() ,
,![]() 點是它的右端點,弦
點是它的右端點,弦![]() 過橢圓的中心
過橢圓的中心![]() ,
,![]() ,
,![]() .
.

(1)求橢圓的標準方程;
(2)設![]() 、
、![]() 為圓上不重合的兩點,
為圓上不重合的兩點,![]() 的平分線總是垂直于
的平分線總是垂直于![]() 軸,且存在實數(shù)
軸,且存在實數(shù)![]() ,使得
,使得![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com