
【題目】圓錐![]() 如圖①所示,圖②是它的正(主)視圖.已知圓
如圖①所示,圖②是它的正(主)視圖.已知圓![]() 的直徑為
的直徑為![]() ,
, ![]() 是圓周上異于
是圓周上異于![]() 的一點,
的一點, ![]() 為
為![]() 的中點.
的中點.
(I)求該圓錐的側面積S;
(II)求證:平面![]() ⊥平面
⊥平面![]() ;
;
(III)若∠CAB=60°,在三棱錐![]() 中,求點
中,求點![]() 到平面
到平面![]() 的距離.
的距離.

【答案】(1)![]() ;(2)參考解析;(3)
;(2)參考解析;(3)![]()
【解析】試題分析:由圓錐的正視圖可知,圓錐的底面直徑為2,高為2,(1)所以圓錐的母線長![]() ,由圓錐的側面積公式
,由圓錐的側面積公式![]() .本小題的關鍵是應用根據三視圖得到圓錐的半徑以及圓錐的高,從而運用圓錐的側面積公式.
.本小題的關鍵是應用根據三視圖得到圓錐的半徑以及圓錐的高,從而運用圓錐的側面積公式.
(2)欲證平面PAC![]() 平面POD.由判定定理可知,轉化為線面垂直.通過觀察確定直線AC垂直平面PDO.由已知即可得到結論.
平面POD.由判定定理可知,轉化為線面垂直.通過觀察確定直線AC垂直平面PDO.由已知即可得到結論.
(3)點A到平面PCB的距離,,利用![]() ,分別計算出
,分別計算出![]() .即可得到點A到平面PCB的距離.
.即可得到點A到平面PCB的距離.
試題解析:(1)由正(主)視圖可知圓錐的高![]() ,圓
,圓![]() 的直徑為
的直徑為![]() ,故半徑
,故半徑![]() .∴圓錐的母線長
.∴圓錐的母線長![]() ,
,
∴圓錐的側面積![]() .
.
(2)證明:連接![]() ,∵
,∵![]() ,
, ![]() 為
為![]() 的中點,
的中點,
∴![]() .∵
.∵![]() ,
, ![]() ,∴
,∴![]() .又
.又![]() ,
,
∴![]() .又
.又![]() ,
,![]() 平面
平面![]() 平面
平面![]()
(3)![]() ,又
,又![]() ,
,![]() 利用等體積法可求出距離,
利用等體積法可求出距離, ![]()


科目:高中數學 來源: 題型:
【題目】數列{an}中,a1=1,Sn表示前n項和,且Sn , Sn+1 , 2S1成等差數列.
(1)計算S1 , S2 , S3的值;
(2)根據以上結果猜測Sn的表達式,并用數學歸納法證明你的猜想.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列4個求導運算,其中正確的個數是( ) ①(x+ ![]() )′=1+
)′=1+ ![]() ;
;
②(log2x)′= ![]() ;
;
③(3x)′=3xlog3e;
④(x2cos2x)′=﹣2xsin2x.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sin(3ωx+ ![]() ),其中ω>0
),其中ω>0
(1)若f(x+θ)是周期為2π的偶函數,求ω及θ的值;
(2)若f(x)在(0, ![]() ]上是增函數,求ω的最大值;
]上是增函數,求ω的最大值;
(3)當ω= ![]() 時,將函數f(x)的圖象向右平移
時,將函數f(x)的圖象向右平移 ![]() 個單位,再向上平移1個單位,得到函數y=g(x)的圖象,若y=g(x)在[0,b](b>0)上至少含有10個零點,求b的最小值.
個單位,再向上平移1個單位,得到函數y=g(x)的圖象,若y=g(x)在[0,b](b>0)上至少含有10個零點,求b的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】解答題
(1)已知全集U=R,集合A={x|x<﹣4,或x>1},B={x|﹣3≤x﹣1≤2},求A∩B、(UA)∪(UB);
(2)求值:若x>0,求 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若f(x)=x2﹣2x﹣4lnx,則f′(x)>0的解集為( )
A.(0,+∞)
B.(﹣1,0)∪(2,+∞)
C.(2,+∞)
D.(﹣1,0)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=ax3+bx2+cx的極小值為﹣8,其導函數y=f′(x)的圖象經過點 ![]() ,如圖所示,
,如圖所示, 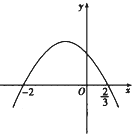
(1)求f(x)的解析式;
(2)若對x∈[﹣3,3]都有f(x)≥m2﹣14m恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學用“五點法”畫函數![]() 在某一個周期內的圖象
在某一個周期內的圖象
時,列表并填入了部分數據,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 5 |
| 0 |
(Ⅰ)請將上表數據補充完整,填寫在答題卡上相應位置,并直接寫出函數![]() 的解
的解
析式;
(Ⅱ)將![]() 圖象上所有點向左平行移動
圖象上所有點向左平行移動![]()
![]() 個單位長度,得到
個單位長度,得到![]() 的圖
的圖
象. 若![]() 圖象的一個對稱中心為
圖象的一個對稱中心為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com