
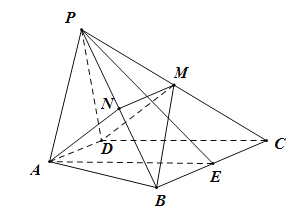
【題目】如圖,四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為等邊三角形,
為等邊三角形,![]() 是棱
是棱![]() 上一點.
上一點.

(1)證明:![]() ;
;
(2)若![]() 平面
平面![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)取![]() 中點為
中點為![]() ,連結
,連結![]() ,
, ![]() ,通過證明
,通過證明![]() 平面
平面![]() ,可得
,可得![]() ;
;
(2)過![]() 作
作![]() ,設
,設![]() ,連
,連![]() ,
,![]() ,利用直線與平面平行的性質定理可得
,利用直線與平面平行的性質定理可得![]() ,又
,又![]() ,所以四邊形
,所以四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點,再通過計算可得
的中點,再通過計算可得![]() ,從而可得
,從而可得![]() 到平面
到平面![]() 的距離為
的距離為![]() ,然后根據體積公式可得結果.
,然后根據體積公式可得結果.
(1)取![]() 中點為
中點為![]() ,連結
,連結![]() ,
, ![]() .
.
因為![]() 為等邊三角形,
為等邊三角形,![]() ,
,
因為![]() ,所以
,所以![]() ,
,
又因為![]() ,
,
所以四邊形![]() 為平行四邊形,
為平行四邊形,
因為![]() ,所以四邊形
,所以四邊形![]() 為矩形,即
為矩形,即![]() ,
,
因為![]() 且
且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因為![]() 平面
平面![]() ,所以
,所以![]() .
.
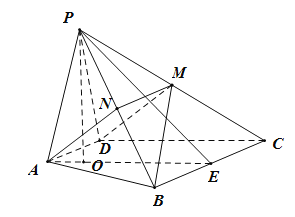
(2)過![]() 作
作![]() ,設
,設![]() ,連
,連![]() ,
,![]() ,則四邊形
,則四邊形![]() 為平面四邊形,
為平面四邊形,
因為![]() 平面
平面![]() ,所以
,所以![]() ,
,
因為![]() ,
,![]() ,所以
,所以![]() ,所以四邊形
,所以四邊形![]() 為平行四邊形,
為平行四邊形,
所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
所以![]() 為
為![]() 的中位線,即
的中位線,即![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點,
的中點,
由(1)知![]() 平面
平面![]() ,因為
,因為![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
作![]() 于點
于點![]() ,因為平面
,因為平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因為![]() 為等邊三角形且
為等邊三角形且![]() ,點
,點![]() 為
為![]() 的中點,所以
的中點,所以![]() ,
,
在![]() 中,因為
中,因為![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 到平面
到平面![]() 的距離為
的距離為![]() ,
,
所以![]() .
.


 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知曲線![]() ,曲線
,曲線![]() ,P是平面上一點,若存在過點P的直線與
,P是平面上一點,若存在過點P的直線與![]() 都有公共點,則稱P為“C1—C2型點”.
都有公共點,則稱P為“C1—C2型點”.
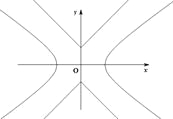
(1)在正確證明![]() 的左焦點是“C1—C2型點”時,要使用一條過該焦點的直線,試寫出一條這樣的直線的方程(不要求驗證);
的左焦點是“C1—C2型點”時,要使用一條過該焦點的直線,試寫出一條這樣的直線的方程(不要求驗證);
(2)設直線![]() 與
與![]() 有公共點,求證
有公共點,求證![]() ,進而證明原點不是“C1—C2型點”;
,進而證明原點不是“C1—C2型點”;
(3)求證:圓![]() 內的點都不是“C1—C2型點”.
內的點都不是“C1—C2型點”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程為
的參數方程為![]() (其中
(其中![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若點![]() 在直線
在直線![]() 上,且
上,且![]() ,求直線
,求直線![]() 的斜率;
的斜率;
(2)若![]() ,求曲線
,求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小王于2015年底貸款購置了一套房子,根據家庭收入情況,小王選擇了10年期每月還款數額相同的還貸方式,且截止2019年底,他沒有再購買第二套房子.下圖是2016年和2019年小王的家庭收入用于各項支出的比例分配圖,根據以上信息,判斷下列結論中正確的是( )
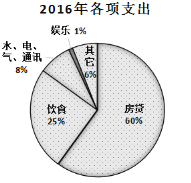
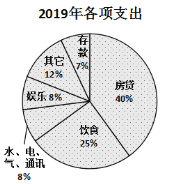
A.小王一家2019年用于飲食的支出費用跟2016年相同
B.小王一家2019年用于其他方面的支出費用是2016年的3倍
C.小王一家2019年的家庭收入比2016年增加了1倍
D.小王一家2019年用于房貸的支出費用比2016年減少了
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】足球運動被譽為“世界第一運動”.為推廣足球運動,某學校成立了足球社團由于報名人數較多,需對報名者進行“點球測試”來決定是否錄取,規則如下:
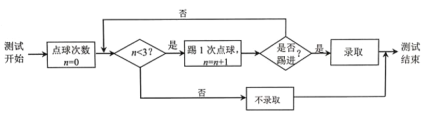
(1)下表是某同學6次的訓練數據,以這150個點球中的進球頻率代表其單次點球踢進的概率.為加入足球社團,該同學進行了“點球測試”,每次點球是否踢進相互獨立,將他在測試中所踢的點球次數記為![]() ,求
,求![]() ;
;
![]()
(2)社團中的甲、乙、丙三名成員將進行傳球訓練,從甲開始隨機地將球傳給其他兩人中的任意一人,接球者再隨機地將球傳給其他兩人中的任意一人,如此不停地傳下去,且假定每次傳球都能被接到.記開始傳球的人為第1次觸球者,接到第n次傳球的人即為第![]() 次觸球者
次觸球者![]() ,第n次觸球者是甲的概率記為
,第n次觸球者是甲的概率記為![]() .
.
(i)求![]() ,
,![]() ,
,![]() (直接寫出結果即可);
(直接寫出結果即可);
(ii)證明:數列![]() 為等比數列.
為等比數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 將
將![]() 的圖象上所有點向左平移
的圖象上所有點向左平移![]() 個單位,然后縱坐標不變,橫坐標縮短為原來的
個單位,然后縱坐標不變,橫坐標縮短為原來的![]() ,得到函數
,得到函數![]() 的圖象.若
的圖象.若![]() 為偶函數,且最小正周期為
為偶函數,且最小正周期為![]() ,則( )
,則( )
A.![]() 圖象與
圖象與![]() 對稱B.
對稱B.![]() 在
在![]() 單調遞增
單調遞增
C.![]() 在
在![]() 有且僅有3個解D.
有且僅有3個解D.![]() 在
在![]() 有僅有3個極大值點
有僅有3個極大值點
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知x與y之間的幾組數據如表:
x | 1 | 2 | 3 | 4 |
y | 1 | m | n | 4 |
如表數據中y的平均值為2.5,若某同學對m賦了三個值分別為1.5,2,2.5,得到三條線性回歸直線方程分別為![]() ,
,![]() ,
,![]() ,對應的相關系數分別為
,對應的相關系數分別為![]() ,
,![]() ,
,![]() ,下列結論中錯誤的是( )
,下列結論中錯誤的是( )
參考公式:線性回歸方程![]() 中,其中
中,其中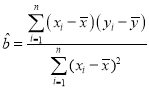 ,
,![]() .相關系數
.相關系數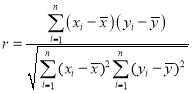 .
.
A.三條回歸直線有共同交點B.相關系數中,![]() 最大
最大
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com